Negative Conclusion from Affirmative Premisses
Alias: Negative Conclusion with No Negative Premiss*
Taxonomy: Logical Fallacy > Formal Fallacy > Syllogistic Fallacy > Negative Conclusion from Affirmative Premisses
Sibling Fallacy: Affirmative Conclusion from a Negative Premiss
Form:
Any form of categorical syllogism with a negative conclusion and affirmative premisses.
| Example | Counter-Example |
|---|---|
| All pets are tame animals.
Some birds are pets. Therefore, some birds are not tame. |
All dogs are animals.
Some pets are dogs. Therefore, some pets are not animals. |
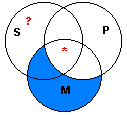
Venn Diagram:
This diagram shows that both the Example and Counter-Example are invalid, since it fails to show that there is anything in the area with the question mark.
Syllogistic Rule Violated:
Any validating form of categorical syllogism with both premisses affirmative has an affirmative conclusion.
Exposition:
Inferring a negative conclusion in a syllogistic argument that has no negative premisses is a formal fallacy of categorical syllogisms. This is a type of rule-breaking fallacy, and the rule broken by an argument of this form is that shown just above. All validating forms of categorical syllogism that have a negative conclusion also have exactly one negative premiss, which can be shown by inspection of the 256 different forms of categorical syllogism. However, it's intuitive that if a negation appears in the conclusion then at least one premiss should be negative. However, this does not necessarily generalize to other systems of logic, so one should not assume that just any argument with a negative conclusion and no negative premisses commits this fallacy, that is, the fallacy applies only to categorical syllogisms.
Exposure:
- Because this is a rule-breaking fallacy, it may not be commonly committed by real-life arguments. The Example given above is meant to be a plausible instance of the fallacy, but whatever plausibility it has may be due to the fact that all of the statements in it are true. The Counter-Example, in contrast, is an argument with the same form that has true premisses and a false conclusion, and thus is invalid. An additional point to keep in mind about the Example and Counter-Example is that any categorical syllogism with two affirmative premisses and a negative conclusion commits the fallacy, not just those of this specific form.
- Every form of categorical syllogism that has affirmative premisses and a negative conclusion breaks some syllogistic rule in addition to the one that defines the fallacy, which can be seen as follows. There are only two types of affirmative categorical proposition: A and I. Any argument with two I premisses would have an undistributed middle term, since both terms in an I proposition are undistributed, so that all such arguments would commit the fallacy of undistributed middle.
Similarly, there are two types of negative categorical proposition: E and O, each of which has at least one distributed term. If the premisses of an argument were an A and an I proposition, then only one term would be distributed in the premisses, namely, the subject term of the A proposition. However, since at least one of the major or minor term will be distributed in the conclusion, such an argument will either commit an illicit process or have an undistributed middle, that is, if the term distributed in the A premiss is distributed in the conclusion, then the middle term must be undistributed. Whereas, if the middle term is distributed in the premisses, then either the major term or both terms of the conclusion will be undistributed in the premisses but distributed in the conclusion.
In an argument with an E conclusion, both the major and minor terms would be distributed. As we have seen, to avoid an illicit distribution, both premisses would have to be A propositions. But then the two terms of the conclusion would have to be the subject terms of the premisses, which means that the middle term would have to be the predicate term of both premisses, which are undistributed. Therefore, any argument with an E conclusion and A premisses will commit a fallacy of distribution.
Thus, to avoid any fallacy of distribution, the premisses will have to be A propositions and the conclusion an O. However, such an argument has universal premisses and a particular conclusion, thus committing the existential fallacy.
In conclusion, every argument that commits the fallacy of negative conclusion from affirmative premisses will commit either a fallacy of distribution or the existential fallacy. Therefore, as long as one recognizes the existence of the existential fallacy, negative conclusion from affirmative premisses is a redundant fallacy. Moreover, as noted above, it is a rather unintuitive type of mistake to make, and probably rare in real-life argumentation.
*Note: J. L. Mackie, "Fallacies", The Encyclopedia of Philosophy, Paul Edwards, Editor in Chief, (1972), p. 171