Affirmative Conclusion from a Negative Premiss
Taxonomy: Logical Fallacy > Formal Fallacy > Syllogistic Fallacy > Affirmative Conclusion from a Negative Premiss
Form:
Any form of categorical syllogism with an affirmative conclusion and at least one negative premiss.
Example:
The indeterminist believes that no caused acts are free, that some human acts are uncaused, and hence, some human acts are free. (Source: A philosophy exam, University of Miami, 4/4/1975)1
Counter-Example:
No cats are marsupials.
Some mammals are not cats.
Therefore, some mammals are marsupials.
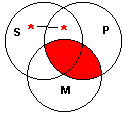
Venn Diagram:
This diagram represents both the Example and Counter-Example, and shows that neither is valid, since the conclusion, "Some S is P", is not shown to be true, for the asterisk might be in the portion of S outside of P. Note that this diagram does not show every instance of the fallacy to be invalid, since other instances may have different forms, and a single Venn diagram can represent only one form.
Syllogistic Rule Violated:
All validating forms of categorical syllogism which have at least one negative premiss also have a negative conclusion.
Exposition1:
Inferring an affirmative conclusion in a syllogistic argument that has at least one negative premiss is a formal fallacy in the logic of categorical syllogisms―for a short introduction to categorical syllogisms, see the entry for syllogistic fallacy. This is because all validating forms of categorical syllogism that have at least one negative premiss also have a negative conclusion, which can be shown by inspection since there are only 256 different forms of categorical syllogism. However, it's intuitive that a negation in the premisses should lead a validly drawn conclusion to also be negative.
Analysis of the Example: The indeterminist's argument is given as follows:
No caused acts are free.
Some human acts are not caused.
Therefore, some human acts are free.
This is a categorical syllogism, and both premisses are negative, specifically, the first premiss is an E-type categorical proposition and the second is an O-type. In contrast, the conclusion is affirmative, specifically, an I-type proposition. Thus, the argument commits the fallacy of Affirmative Conclusion from a Negative Premiss. As if that weren't enough, it also commits the fallacy of Exclusive Premisses, since both premisses are negative. This is a doubly bad argument!
Notes:
- Howard Pospesel, Introduction to Logic: Predicate Logic (1976), p. 178
- See, also: Irving M. Copi & Carl Cohen, Introduction to Logic (Tenth Edition, 1998), p. 277-8