Exclusive Premisses
Taxonomy: Logical Fallacy > Formal Fallacy > Fallacy of Syllogistic Logic > Exclusive Premisses
Alias: Two Negative Premisses1
Form: Any form of categorical syllogism with two negative premisses.
| Example | Counter-Example |
|---|---|
| No moslems are atheists.
No christians are moslems. Therefore, no christians are atheists. |
No reptiles are mammals.
No dogs are reptiles. Therefore, no dogs are mammals. |
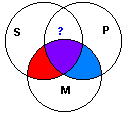
Venn Diagram:
This diagram represents both the Example and Counter-Example, which it shows to be invalid, since the area with the question mark is not shown to be empty.
Syllogistic Rule Violated:
At least one premiss of a valid categorical syllogism is affirmative.
Exposition2:
Exclusive Premisses is a type of rule-breaking fallacy in the logic of categorical syllogisms. The rule broken by an argument of this form is that shown just above. It just so happens that no categorical syllogism with two negative premisses has a validating form. This fact does not necessarily generalize to other systems of logic, so one should not assume that just any argument with two negative premisses commits the fallacy.
Also, because this is a rule-breaking fallacy, it may not be commonly committed by real-life arguments. The Example given above is meant to be a plausible instance of the fallacy, but whatever plausibility it has may be due to the fact that its conclusion is true. The Counter-Example, in contrast, is an argument with the same form that has true premisses and a false conclusion, and thus is invalid. An additional point to keep in mind about the Example and Counter-Example is that any categorical syllogism with two negative premisses commits the fallacy, not just those of this specific form.
Notes:
- W. Kent Wilson, "Formal Fallacy", The Cambridge Dictionary of Philosophy, Robert Audi, General Editor (1995), p. 317
- See, also: Irving M. Copi & Carl Cohen, Introduction to Logic (Tenth Edition, 1998), p. 277