Illicit Contraposition
Taxonomy: Logical Fallacy > Formal Fallacy > Quantificational Fallacy > Illicit Contraposition
| Forms | |
|---|---|
| E | I |
| No S are P.
Therefore, no non-P are non-S. |
Some S are P.
Therefore, some non-P are non-S. |
| Venn Diagrams | |
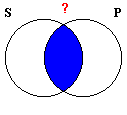 |
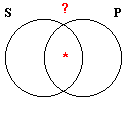 |
| Similar Validating Forms | |
| A | O |
| All P are Q.
Therefore, all non-Q are non-P. |
Some P are not Q.
Therefore, some non-Q are not non-P. |
| Examples | |
| No conservatives are liberals.
Therefore, no non-liberals are non-conservatives. |
Some dogs are pets.
Therefore, some non-pets are non-dogs. |
| Counter-Examples | |
| No dogs are cats.
Therefore, no non-cats are non-dogs. |
Some physical things are invisible.
Therefore, some visible things are non-physical. |
Exposition1:
"Illicit contraposition" is not a scandal from the Reagan administration2. Rather, "contraposition" refers to the process of switching the subject and predicate terms of a categorical proposition, and negating each. For instance, consider the categorical A proposition "All bats are mammals": "Bats" is its subject term and "Mammals" is its predicate term, negating these terms produces "Non-bats" and "Non-mammals", and switching their positions in the proposition produces: "All non-mammals are non-bats."
Contraposition is a validating form of immediate inference for A and O categorical propositions. In fact, these two types of proposition are logically equivalent to their contrapositives, which is what the result of contraposition is called. This means that you can validly infer a contrapositive from an A or O proposition, and vice versa.
However, contraposition is a non-validating form of inference for E and I propositions. So, E and I propositions are not as a general rule logically equivalent to their contrapositives, and it is generally invalid to infer a contraposition from an E or I proposition, or the reverse. Hence, contraposing an E or I proposition is an illicit contraposition. See the Table, above, for both the illicit contrapositions, under "Forms", and the licit ones, under "Similar Validating Forms".
Exposure:
The Venn Diagrams above show that the two forms of Illicit Contraposition are not validating. The diagram for the E proposition shows that no S is P―which is indicated by the blue shading of the overlap of the S and P circles―but it fails to show that there is nothing in the area outside both circles, which is the overlap of the non-S and non-P areas. A question mark in an area means that it might or might not be empty. Similarly, the diagram for the I proposition shows that some S is P, but fails to show that there is anything in the area outside both circles.
Moreover, the Counter-Examples above show that the forms are not validating, since each has an instance with a true premiss and a false conclusion. It's harder to find a Counter-Example to the contraposition of I propositions than E ones since, in order for the conclusion of such an I inference to be false, the two classes must jointly exhaust the universe but not be mutually exclusive. In the Counter-Example, the premiss is true because there are invisible physical things, such as atoms; but the conclusion is false because there are no visible things that are not physical.
Notes:
- Patrick J. Hurley, A Concise Introduction to Logic (Fifth Edition) (Wadsworth, 1994), p. 214.
- Thanks to John Congdon for the "contra" joke.