Illicit Conversion
Alias: False Conversion1
Taxonomy: Logical Fallacy > Formal Fallacy > Quantificational Fallacy > Illicit Conversion
Example:
We like the beautiful and don't like the ugly; therefore, what we like is beautiful, and what we don't like ugly….2
| Forms | |
|---|---|
| All P are Q.
Therefore, all Q are P. |
Some P are not Q.
Therefore, some Q are not P. |
| Examples | |
| All communists are atheists.
Therefore, all atheists are communists. |
Some dogs are not pets.
Therefore, some pets are not dogs. |
| Counter-Examples | |
| All dogs are mammals.
Therefore, all mammals are dogs. |
Some mammals are not cats.
Therefore, some cats are not mammals. |
Exposition3:
Illicit conversion does not refer to unlawful changing of religion. Rather, "conversion" is the name given in the logic of categorical propositions to the switching of the subject and predicate terms. The table below shows the four traditional categorical propositions, together with their conversions, and whether the original proposition is logically equivalent to its converse.
| Type | Form | Converse | Venn Diagram | Equivalent? |
|---|---|---|---|---|
| A | All S is P. | All P is S.4 | 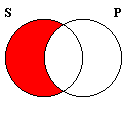 | No |
| E | No S is P. | No P is S. | 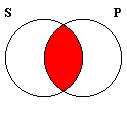 | Yes |
| I | Some S is P. | Some P is S. | 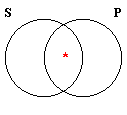 | Yes |
| O | Some S is not P. | Some P is not S. | 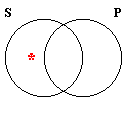 | No |
As can be seen from the table, the E and I propositions are equivalent to their converses, which means that conversion is a validating form of immediate inference for E and I categorical propositions. In contrast, conversion is non-validating for the A and O propositions. Hence, to commit the traditional fallacy of Illicit Conversion is to convert an A or O proposition.
The Venn diagrams of the Forms included in the table also show that the two forms equivalent to their converses are those that are symmetrical―E and I―while the two asymmetrical ones are non-equivalent to their converses―A and O. This, of course, is because conversion switches the subject and predicate terms.
Exposure:
Originally, as explained in the Exposition and Subfallacy sections, above, illicit conversion was considered a fallacy in the Aristotelian logic of categorical propositions. However, there is no reason why the fallacy shouldn't be extended to quantified statements that go beyond the original four. For this reason, I classify this as a fallacy of quantificational logic rather than one of categorical logic, since the traditional logic of categorical statements is subsumed within quantificational logic.
For example, consider the statement: "Every man loves some woman", which is not an A statement―though it looks superficially like one―because it contains two quantifiers: "every" and "some". Nonetheless, it is not equivalent to its converse: "Everyone who loves some woman is a man." Thus, it would be just as much an illicit conversion to reason from the former to the latter.5
Analysis of the Example: This is really two arguments, both of which have the same general form, packed into one:
- We like the beautiful, therefore what we like is beautiful.
- We don't like the ugly, therefore what we don't like is ugly.
"We like the beautiful" means that whatever is beautiful we like. In other, more stilted, words: all beautiful things are things that we like. In contrast, "what we like is beautiful" means that whatever we like is beautiful, that is, all things that we like are beautiful things. So, the first argument reworded is:
All beautiful things are things that we like.
Therefore, all things that we like are beautiful things.
Clearly, this argument commits an illicit conversion. The invalidity of the argument may have been concealed from Ives by the confusingly similar wording of the premiss and conclusion. Similar considerations apply to the second argument.
Notes:
- Madsen Pirie, How to Win Every Argument: The Use and Abuse of Logic (2006), pp. 74-6.
- Charles Ives, Essays Before a Sonata, The Majority, and Other Writings, edited by Howard Boatwright (New York: W. W. Norton & Co., Inc., 1962), p. 77. Via: Howard Pospesel, Introduction to Logic: Predicate Logic (1976), p. 176.
- The Encyclopedia of Philosophy, Paul Edwards, Editor in Chief (Macmillan, 1972), Volume 3, pp. 170-1 and Volume 5, p. 37.
- Aristotle made a distinction between two types of conversion that subsequent logicians have dubbed "simple" and "per accidens". Simple conversion is what is called simply "conversion", above, namely the switching of the subject and predicate terms. Conversion per accidens involved not only switching the terms but changing the quantity of the proposition from universal to particular. So, the conversion per accidens of the A proposition "All bats are mammals" would be "Some mammals are bats". Since E propositions fully convert, only the A propositions could be converted per accidens, and traditional logicians claimed that such conversion was valid. As a result, converting an A proposition was identified as "the fallacy of simple conversion of an A statement". However, from a modern point of view, conversion per accidens commits the existential fallacy. See:
- Thomas P. Kiernan, Aristotle Dictionary (1962), under "Propositions, Conversion of".
- William Angus Sinclair, The Traditional Formal Logic: A Short Account for Students (Fifth Edition, 1963), p. 38n.
- For those who know quantificational logic, "Every man loves some woman" can be translated as:
∀x[Mx → ∃y(Wy & Lxy)]
Where "Mx" means "x is a man", "Wy" means "y is a woman", and "Lxy" means "x loves y". Whereas, "Everyone who loves some woman is a man" can be translated as:
∀x[∃y(Wy & Lxy) → Mx]
Since the difference between these two statements is the reversal of the direction of the arrow within the scope of a universal quantifier, this is a conversion; and, since the statements are not equivalent, it is therefore an illicit one.