Illicit Major
Alias: Illicit Process of the Major Term*
Taxonomy: Logical Fallacy > Formal Fallacy > Syllogistic Fallacy > Illicit Process > Illicit Major
Sibling Fallacy: Illicit Minor
Form:
Any form of categorical syllogism in which the major term is distributed in the conclusion, but not in the major premiss.
| Example | Counter-Example |
|---|---|
| All communists are leftists.
No conservatives are communists. Therefore, no conservatives are leftists. |
All dogs are animals.
No cats are dogs. Therefore, no cats are animals. |
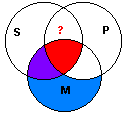
Venn Diagram:
This diagram represents both the Example and Counter-Example. It does not show the conclusion, "No S is P", to be true, because the area with the question mark is not shown to be empty. Therefore, both the Example and Counter-Example are invalid.
Exposition:
An "illicit process of the major" is not an illegal trial of a military officer, rather it is a syllogistic fallacy in which the major term is undistributed in the major premiss, but distributed in the conclusion, which is the "illicit process"—that is, "illicit" distribution of the major term.
The major term in the Example, above, is "leftists" since it is the predicate term of the conclusion. "Leftists" is distributed in the conclusion because the predicate term of an E-type proposition is distributed. The major premiss of the Example is the first premiss, since it contains the major term. "Leftists" is undistributed in the major premiss since the predicate term of an A-type proposition is undistributed. Thus, there is an illicit distribution of the major term in the Example.
The same points apply to the Counter-Example, except that its major term is "animals". The difference between the Example and the Counter-Example is that the former is intended to be at least somewhat plausible. In contrast, the Counter-Example has obviously true premisses and a clearly false conclusion, which means that it is invalid. However, the Example is also invalid, and whatever plausibility it has probably comes from the fact that its conclusion is true.
*Note: See also: Irving Copi & Carl Cohen, Introduction to Logic (Tenth Edition) (Prentice Hall, 1998), pp. 276-7.