Some Are/Some Are Not
Alias: Unwarranted Contrast1
Taxonomy: Logical Fallacy > Formal Fallacy > Fallacy of Quantificational Logic > Some Are/Some Are Not
| Some S are P.
Therefore, some S are not P. |
Some S are not P.
Therefore, some S are P. |
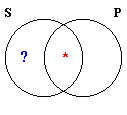
Venn Diagram:
This diagram is for the first form above. A diagram for the second form is obtained by taking circle P to represent non-P. The diagram shows this form of argument to be non-validating, because the area with a question mark may be empty, so far as the premiss indicates.
Example:
Some politicians are crooks.
Therefore, some politicians are not crooks.
Exposition:
To understand the nature of this fallacy, one needs to know the difference between logical implication and conversational implicature:
- Implication: This is a relation between propositions, that is, sentences that are true or false.
- Implicature: This is a relation between the fact that someone makes a statement and a proposition.
For example, suppose that I state that today is Sunday and it's raining. This statement logically implies―in the sense of 1, above―that it's raining. In contrast, the fact that I made the statement implicates―in the sense of 2, above―that I believe that it's raining. The statement taken by itself implies nothing about what I believe, but the fact that I made the statement implicates that I believe it. In other words, I didn't say that I believe it's raining, but from the fact that I said it's raining you can infer that I believe it.
Why does the fact that I made the statement implicate that I believe it? All conversational implicature is based on certain rules―or "maxims", as the philosopher Paul Grice called them2―which govern cooperative communication. One of these rules is that you should state only what you believe―which Grice called a maxim of "Quality". Thus, from the fact that I state something, you can conclude that I believe it. Of course, it's possible that I might say it's raining but not believe it, in which case I would have lied. This is one way in which implicature differs from implication, since implicature is based upon the assumption that people are trying to cooperate by obeying the rules.
How does this relate to the Fallacy of Some Are/Some Are Not? There is another rule of conversation―called by Grice a maxim of "Quantity"―that one should make statements as logically strong as is consistent with telling the truth. So, while a statement of the form "Some S are P" does not logically imply "Some S are not P", the fact that someone makes the former statement conversationally implicates the latter. In other words, if one knows that all S are P one should say so, and the fact that one says only that some are implicates that one does not believe that all are. This latter fact, together with the assumption that you are telling the truth, implicates that not all S are P.
Thus, the theory of conversational implicature explains how it is possible to mislead while still speaking the literal truth: by means of what we call "half-truths" we can implicate falsehoods with our statements. If we know that all S are P, then the statement that some are is a half-truth. Half-truths are wholly true, since truth and falsity do not come in degrees, but they are misleading because they violate norms of efficient communication. Hence, the legal oath to tell the truth (Quality), the whole truth (Quantity), and nothing but the truth.
So, what is the Fallacy of Some Are/Some Are Not? It is the mistake of confusing logical implication and conversational implicature by thinking that "some are" statements logically imply "some are not" statements, when the former statements only conversationally implicate the latter.
Exposure:
Now, you may think that the theory of conversational implicature is all very interesting, and that you see how it explains how one can mislead with "half-truths", but you're still not convinced that Some Are/Some Are Not is a logical fallacy. It may still seem to you that "some S are P" logically implies "some S are not P", not just conversationally implicates it.
You may also intuitively feel that "all S are P" logically implies "some S are P". However, put these two supposed logical implications together and what do you get? "All S are P" implies "some S are P", which then implies "some S are not P". Therefore, by eliminating the middle man, we get that all S are P implies that some S are not P. So, "all whales are mammals" would logically imply "some whales are not mammals", which is in fact its contradictory! Clearly, something has gone terribly wrong here.
At best, this example shows that at least one of the two supposed logical implications is not a true implication. In fact, neither of these alleged implications is a logical implication, though I will not try to prove that here―see the entry for the Existential Fallacy for more on why the first "implication" does not hold. However, the example ought to go some way in convincing you that intuitions about logical implication are not totally trustworthy.
Notes:
- W. Kent Wilson, "Formal Fallacy", in The Cambridge Dictionary of Philosophy (Second Edition), Robert Audi, General Editor(1995), p. 317. The name "some are/some are not" for this fallacy also comes from this source.
- Paul Grice, "Logic and Conversation", in Studies in the Way of Words (Harvard, 1989), pp. 22-40.