
Undistributed Middle Term
Taxonomy: Logical Fallacy > Formal Fallacy > Syllogistic Fallacy > Undistributed Middle Term
Alias: Undistributed Middle
Form:
Any form of categorical syllogism in which the middle term is not distributed in at least one of the premisses.
Example:
[O]ne patient…concluded that there are money-trees because "money is green [in the United States] and so are trees, so money must grow on trees."
Venn Diagram:
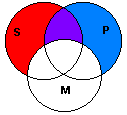
The Example is represented by this diagram, where "S" represents the minor term, "P" is the major term, and "M" the middle term. The diagram does not show the conclusion to be true, which means that the argument is invalid. See the Analysis, below, for details.
Syllogistic Rule Violated:
The middle term of a categorical syllogism must be distributed in at least one premiss.
Exposition:
This is a type of rule-breaking fallacy of categorical syllogisms, and the rule broken by an argument of this form is that shown just above. All forms of categorical syllogism that have an undistributed middle term are non-validating, which can be shown by inspection of the 256 different forms of categorical syllogism.
Unlike some of the other syllogistic rule-breaking fallacies, undistributed middle is occasionally committed by real-life arguments, which may be partly the result of the similarity of the most common form of undistributed middle to a validating form of argument.
Probably the most commonly occurring form of categorical syllogism with an undistributed middle term is the following:
All P are M.
All S are M.
Therefore, All S are P.
In this form, the middle term, M, is undistributed since it is the predicate of both premisses, which are A-type propositions. This is the form exhibited by the argument in the Example―see the Analysis, below, for the details. This form is similar to the validating form of categorical syllogism known as "Barbara":
All M are P.
All S are M.
Therefore, All S are P.
In Barbara, the middle term in the major premiss is distributed, since it is its subject term. These two forms are so similar that they might be confused.
However, an important point to keep in mind is that any categorical syllogism with an undistributed middle term commits the fallacy, not just this specific form. Even some reference works mistakenly treat the above form as the form of undistributed middle, but none of the syllogistic fallacies is limited to a single form of categorical syllogism. For example, the penguin's argument in the cartoon, shown above, is the following:
Some old TV shows are black and white [things].
[All] penguins are black and white [things].
Therefore, some penguins are old TV shows.
Here, the middle term is "black and white [things]", which is undistributed since it is the predicate of affirmative categorical propositions. This argument has the following form which is clearly different from the most common form of undistributed middle:
Some P are M.
All S are M.
Therefore, some S are P.
However, this form is also similar to a validating form that it may be mistaken for:
Some P are M.
All M are S.
Therefore, some S are P.
Exposure:
"Undistributed middle" is the name of one of the most famous fallacies, and is sometimes used as a synonym for "fallacious argument". Some people know that an undistributed middle is somehow logically bad, and mistakenly think that any bad argument must be a case of undistributed middle. In other words, they seem to reason as follows:
All arguments with undistributed middle terms are bad arguments.
This is a bad argument.
Therefore, this argument has an undistributed middle term.
Ironically, this argument is a bad argument because it has an undistributed middle term, namely, "bad arguments"!
Now, strictly speaking, this argument is not a categorical syllogism, since its minor term "this argument" is not a categorical term but a phrase that refers to an individual thing. However, it is traditional to treat names or other denoting phrases that refer to an individual thing as if they are categorical terms. Moreover, a proposition such as "Socrates is a man" is considered to be an A-type proposition, so that "Socrates" is distributed, but "man" is not. Thus, in the argument above, "bad argument" is undistributed in the minor premiss.
Resource:
Irving Copi & Carl Cohen, Introduction to Logic (Tenth Edition) (Prentice Hall, 1998), pp. 275-276.
Analysis of the Example:
Here is a longer excerpt of the book from which the example is taken:
[A] major component of reasoning takes place in a frontal module of the brain, a module being a specialized, relatively independent group of inter-connected nerve cells performing a particular category of tasks. Patients who have an injury confined to this module…have a…specific syndrome in which reason is disturbed without a generalized disorder of cognition. Appropriately enough, this isolated impairment of the module for reason is called "the dysexecutive syndrome," a condition analogous to selective disorders of language (the aphasias) or memory (the amnesias).Patients with the dysexecutive syndrome…make mistakes in assembling rational sequences of thought. For example, one patient with the dysexecutive syndrome concluded that there are money-trees because "money is green [in the United States] and so are trees, so money must grow on trees."
Formulating the patient's argument into a standard form categorical syllogism produces:
All leaves that grow on trees are green things.
All pieces of paper money of the United States are green things.
Therefore, all pieces of paper money of the United States are leaves that grow on trees.
This categorical syllogism has the most common form of undistributed middle as discussed in the Exposition, above.
Source: Donald B. Calne, Within Reason: Rationality and Human Behavior, Pantheon, 1999, pp. 15-16.