Previous Month | RSS/XML | Current | Next Month

WEBLOG

November 30th, 2016 (Permalink)

New Book: Dialogues in Argumentation

Volume 3 in the Windsor Studies in Argumentation series is now available, namely, Dialogues in Argumentation edited by Ron von Burg. This is a collection of papers presented at two different scholarly conferences, so it's not for beginners. It contains papers by such argumentation scholars as Tony Blair, Dale Hample, and Hans Hansen.

November 24th, 2016 (Permalink)

A Big Thanksgiving Thank You!

On this day of thanksgiving, thanks to all of those who have supported The Fallacy Files since last year, whether by clicking on the Google ads or donating directly via the PayPal button on your right! Also, The Fallacy Files is an Amazon Associate. With the holidays approaching, please consider doing any shopping at Amazon by way of one of the links from this website. It won't cost a penny extra and will benefit the site. Thanks to everyone who helped keep The Fallacy Files going for another year!

Update (4/18/2021): The Fallacy Files is no longer an Amazon Associate.

November 23rd, 2016 (Permalink)

A Puzzle for Thanksgiving

This Thanksgiving I'm planning to do something I've never done before, namely, to hold a celebration at my house for family members and prepare a Thanksgiving feast for them.

Unfortunately, as soon as I decided to do this, complications cropped up. Some of my relatives have dietary requirements that must be taken into account. Moreover, some have personal conflicts with others such that they may refuse to attend if others do, but some may fail to come unless others do. After considerable consultation and thought, I was able to reduce all of the constraints on various relatives attending the dinner down to the following five rules.

  1. If either Aunt Alice comes to the dinner or Uncle Bert refuses to attend then Cousin Carl will refuse to come.
  2. If Cousin Carl refuses to attend then I will either roast a turkey or bake a ham or possibly both.
  3. If Aunt Alice doesn't come then Uncle Bert will.
  4. If Uncle Bert comes then I will serve both fish and a baked ham.
  5. If either Aunt Alice comes or I do serve fish then I will roast a turkey if and only if Cousin Carl attends.

Here's what's puzzling me: Should I bake a ham? When you think that you know the answer, click on the solution, below.

Solution

November 15th, 2016 (Permalink)

Lesson in Logic 14: Equivalence

Now that everything but the wailing and gnashing of teeth is over for this election, we can return to our regularly-scheduled programming. The logic lessons got pushed aside in the last couple of months by the debates and other election tomfoolery, but here's the next one in the series on how to read Venn diagrams.

One value of using Venn diagrams to represent statements is to see logical relationships between the statements. For instance, if we draw diagrams for two statements about the same two classes, the diagrams will show whether the two sentences are logically equivalent.

To say that two statements are logically equivalent is to say that they say the same thing in terms of logic. There may well be, and probably will be, subtle differences of nuance in the meanings of the two statements. Equivalent statements do not necessarily, and usually don't, mean exactly the same thing, but only make the same claim, logically speaking. If two categorical statements are logically equivalent, then the Venn diagrams representing the two statements, as you might guess, will be either identical or mirror images of each other―assuming that the circles represent the same classes. Look at the following example.

Example: All bats are non-birds.

Make a Venn diagram of this statement. First, draw the primary diagram, that is, the two overlapping circles. Now, label the two circles, which is a little tricky because the second class term is the complement of the class term "birds". So, there are two ways you can diagram the statement depending on whether you choose "birds" or "non-birds" as the second class. It doesn't matter which you choose, so long as you're consistent. For the sake of this example, label the second circle "birds".

As you should have learned in the last lesson, to represent an A categorical statement―"all S is P"―shade in the part of the subject class, S, that is outside of the predicate class, P, thus showing that any member of S is a member of P. Here, S=bats and P=non-birds. In your diagram, however, the second circle represents birds. As you learned in lesson 11, the complement of a class, P, is the class of everything outside of P. So, the class of non-birds is represented in your diagram by the area outside of the "birds" circle. Thus, to represent the Example sentence, you need to shade the part of the bats circle which is outside of the non-birds area. However, the part of the bats circle that is outside of the non-birds area is the same as the part of the bats circle that is inside of the birds area, which just happens to be the football-shaped overlap area of the diagram. 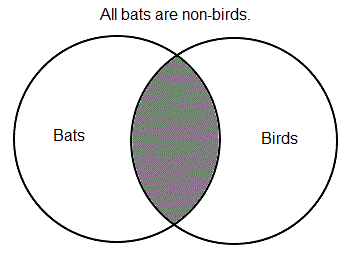So, your diagram should look like this: All bats are non-birds.

Now, if you've been paying attention, you should notice that this is the same diagram that you would draw for the E statement "no bats are birds", which shows that these two statements are logically equivalent. In fact, as a general matter, statements of the form "all S are non-P" are equivalent to statements of the form "no S are P", when S and P represent the same classes in both statements.

In traditional logic, this logical relation between these two types of statement is called "obversion", each statement is said to be the "obverse" of the other, and to replace one such statement by its obverse is said to "obvert" it. To obvert any categorical statement, simply change an A to an E, or vice versa, or an I to an O, or vice versa; also, replace the statement's predicate term with its complement. For example, the obverse of the I statement "some philosophers are logicians" is the O statement "some philosophers are not non-logicians". It should be intuitively obvious that these two statements are equivalent, but you can also draw a Venn diagram of each and they should turn out to be identical.

Rather conveniently, any of the four traditional categorical statements, A, E, I, and O, is logically equivalent to its obverse. You could memorize this fact, together with the definition of "obversion", but one of the advantages of learning to use Venn diagrams is that you won't need to, since you can use diagrams to check whether any two statements are equivalent. The same is true of the traditional equivalences called "conversion" and "contraposition", about which I won't go into detail, but see the following exercises.

Exercises: Use Venn diagrams to determine whether the following pairs of statements are logically equivalent:

1.All bats are mammals.All mammals are bats.
2.Some philosophers are not logicians.Some non-logicians are not non-philosophers.
3.No bats are birds.No birds are bats.
4.Some logicians are philosophers. Some non-philosophers are non-logicians.

Answers to the Exercises

Source: William Angus Sinclair, The Traditional Formal Logic: A Short Account for Students (Fifth Edition, 1963), pp. 35-36 & 38-39

Previous Lessons:

Newsweek Madam President Cover
November 13th, 2016 (Permalink)

Dewey Defeats Truman, Again

One last election-related entry, then maybe we can move on. Among those wringing their hands and rending their garments in the wake of the election are some pollsters and poll-watchers.

A famous photograph shows a beaming President Harry Truman holding up a copy of a newspaper whose headline reads: "Dewey Defeats Truman". Truman, of course, had won. Dewey had led Truman in the polls up to election day, and so the newspaper had proceeded to print up an edition proclaiming Dewey's victory before the votes were counted. As a result, the picture has become a famous cautionary example about the dangers of being misled by polls―I've used it that way, myself; see the Resource, below.

This year, Newsweek magazine has committed a similar gaffe by accidentally releasing copies of its magazine proclaiming Hillary Clinton the next president―see the picture, above. Much the same thing seems to have happened as did with the newspaper: the magazine wanted to get copies of its commemorative edition into bookstores as soon as possible. Apparently, Newsweek prepared issues for both Clinton and Trump but, based on the polls, a distributor printed up and shipped the Clinton issue before the results were in.

So, why is it that the polls seem to have been wrong this election? One thing to keep in mind is that this was a very close election. The popular vote has still not been completely tabulated, but the current difference between the two major candidates is a little over 700,000 out of almost 122 million votes cast. In other words, the difference between the two candidates is less than a single percentage point of the total popular vote.

Not only that, but the candidate who has that small lead is Hillary Clinton! That's right, Donald Trump won the election but Clinton is on the way to winning the popular vote, albeit by a very narrow margin. How is this possible?

Who wins the election is not determined by the popular vote, but by the electoral college. The electoral college is not a college that you attend to become an elector; rather, every state has a certain number of electoral votes, and the winner of the election is the candidate who receives the greatest number of electoral votes. Almost all states are "winner-take-all", which means that if a candidate wins the popular vote in that state that candidate will receive all of the state's electoral votes. If the popular vote winner's supporters are concentrated in a few states, whereas the popular vote loser's supporters are spread out over many states, it's possible that the latter will win more states, and thus more electoral votes than the former.

This is exactly what happened this time around. Clinton's supporters were concentrated in two places: the northeast and the west coast, whereas Trump's supporters were spread all over the rest of the country. As a result, despite the fact that the two candidates received close to the same number of votes, Trump was able to win a decisive number of electors.

The reason I raise these points is that to expect polls to be able to predict such a close election, especially one in which the winner loses the popular vote, is expecting too much. You'd probably have as much success by simply flipping a coin.

Now, many people got the impression from the polls that Clinton was likely, even very likely, to win. However, much of Clinton's lead was in polls earlier in the year, and as we approached the election that apparent lead began to shrink, with some late polls even showing Trump ahead. One thing to keep in mind is that at best polls give evidence of public opinion at the time they are taken. This election year seems to have been a particularly volatile one, as indicated by the polls themselves, so that public opinion may well have changed over time. Perhaps those early polls were just plain wrong, or perhaps public opinion actually shifted as election day neared.

Public opinion polls are not designed to determine the electoral college vote. Those polls that showed Hillary Clinton ahead in the popular vote were in fact correct, though some surely exaggerated the extent of her lead.

I often point out that individual polls are not perfectly precise, which is why they have a margin of error. Thus, it is not shocking that a poll should be off by as much as three percentage points, since this is within the standard margin. I also recommend looking at multiple polls as a way of compensating for the lack of precision in individual ones, but the result of such aggregation is not perfectly precise, either. Polling is not now, and never will be, a precise science. Especially in an election as close as this one, we shouldn't be surprised if polls are off by a few percentage points.

Sources:

Resource: How to Read a Poll

November 7th, 2016 (Permalink)

"Don't Waste Your Vote"

One thing that is unusual in this election year―one of many things―is how disliked the two major candidates are. Here was the situation about five weeks ago:

Hillary Clinton and Donald Trump are the two most disliked presidential nominees in modern American history. That was true at the beginning of this campaign, and, as we sprint toward Election Day, it’s still true now.
Source: Harry Enten, "Trump Is More Unpopular Than Clinton Is―And That Matters", FiveThirtyEight, 9/30/2016

As a result, many of the arguments in favor of voting for one of the two major candidates are actually framed in terms of rejecting the other one. If you pay attention to the election, you will often hear these types of argument made by pundits, surrogates for the candidates, and their supporters. For instance, here's David Gelernter on why he will vote for Trump:

Mrs. Clinton has nothing on Mr. Trump when it comes to character. She lies…the way basketball stars shoot baskets―constantly, nonstop, because it’s the one thing she is best at and (naturally) it gives her pleasure to hear herself lie―swish!―right onto the evening news. … I’ll vote for Mr. Trump―grimly. But there is no alternative, no shadow of a responsible alternative.
Source: David Gelernter, "Trump and the Emasculated Voter", The Wall Street Journal, 10/14/2016

Here's Noam Chomsky, of all people, on why he would vote for Clinton in a "swing state":

If Clinton is nominated and it comes to a choice between Clinton and Trump, in a swing state, a state where it’s going to matter which way you vote, I would vote against Trump, and by elementary arithmetic, that means you hold your nose and you vote Democrat. I don’t think there’s any other rational choice.
Source: "Chomsky on Supporting Sanders & Why He Would Vote for Clinton Against Trump in a Swing State", Democracy Now!, 5/16/2016

We hear this sort of argument every four years, but this year, because of the unprecedented unpopularity of the two major candidates, it seems to be the main political argument. Here is its logical form:

  1. You should vote for one of the two major-party candidates for president: A or B.
  2. You should not vote for candidate A.
  3. Therefore, you should vote for candidate B.

In other words, the argument has two premisses, one of which is a disjunction. The second premiss denies one of the two disjuncts. Therefore, the argument concludes that the other disjunct must be true. The form of this argument is disjunctive syllogism (DS), which is a syllogism because it has two premisses, and disjunctive because one premiss is a disjunction. DS is a validating form of argument, that is, every argument of this form is valid. Thus, the argument above is valid. Note: The account in the above paragraph is not quite correct; see the Technical Note, below, for details.

So, what if anything is wrong with this argument? Validity isn't everything: all validity means is that if the premisses are true then the conclusion is true. But are the premisses true?

I won't address the question of who's worse; you'll have to make up your own mind about that. Rather, it's the other premiss that I want to examine, that is, the disjunctive premiss. Specifically, is it true that you should vote for one of the two major party candidates?

If the disjunctive premiss is false―that is, if there are one or more alternatives that it leaves out―then the argument is unsound. Moreover, it commits the black-or-white fallacy, also known as a false dilemma, among other names―see the Fallacy, below, for details. Note: Again, this is not quite correct; see the Technical Note, below, for details.

There are other candidates running, including Gary Johnson of the Libertarian Party and Jill Stein of the Green Party. What would the argument look like if we included one or more of these candidates? Let's add Johnson as an alternative, and look at the pro-Clinton version of the argument just as an example:

  1. You should vote for Clinton or Trump or Johnson for president.
  2. You should not vote for Trump.
  3. Therefore, you should vote for Clinton for president.

This argument is invalid! Also, it lacks the form of a DS, though it superficially looks like one. A validly-drawn conclusion would be: You should vote for Clinton or Johnson for president. Indeed, a Johnson supporter could make the following alternative argument:

  1. You should vote for Clinton or Trump or Johnson for president.
  2. You should vote for neither Clinton nor Trump.
  3. Therefore, you should vote for Johnson for president.

Of course, people such as Gelernter and Chomsky, who argue that you should vote for either Clinton or Trump, at least in "swing states", are aware that there are other candidates on the ballot. They didn't just forget that Johnson and Stein are running. Instead, they think that you should vote for one of the two major-party candidates, that is, they think that the first premiss of the original argument is true, at least when the chips are down. Why do they believe this?

The usual argument against voting for a third-party or independent candidate is that to do so would be to "throw away" or "waste" your vote. But in what sense would it be a "waste"? Couldn't you argue just as well that to vote for a candidate you despise or think is unfit for the office is to "throw away" your vote?

Some claim that candidates such as Johnson and Stein are not real alternatives. However, Gary Johnson, the Libertarian candidate, is on the ballot in all fifty states. All that is necessary for him to be elected is for more voters to vote for him than for any other candidate. In this respect, he is exactly like Clinton and Trump. The Green Party candidate, Jill Stein, is on the ballot in 44 states, which is enough that she has a mathematical chance of acquiring enough electors to win the election. Again, all that's needed is that enough people vote for her.

I'm not naive about the chance of a third-party candidate actually winning the election. Recent polls show that both Johnson and Stein each have only single-digit support. However, part of the reason why this is so is that so many voters have bought into the claim that third parties can't win. It's a self-fulfilling prophecy: as long as most voters believe it, they won't "throw away" their votes on minor-party candidates. If it's true that third-party candidates can't win, a large part of the reason is simply because people continue to believe and act as if it's true.

I certainly wouldn't bet on either Johnson or Stein winning tomorrow. But this isn't a gambling game, it's an election. The way that an election is supposed to work is that you vote for the person you think is the best of the available choices, not the one you think is most likely to win. Your vote is neither "wasted" nor "thrown away" because the candidate you vote for isn't elected.

Now, I'm not telling you who to vote for tomorrow. If you think Clinton is the best candidate, then vote for her; if you prefer Trump, then vote for him. If you don't like either one of them, but like Johnson or Stein even less, then you're on your own. What I'm trying to do is to counter the specious argument that you must vote for one of the two major party candidates even if you have to hold your nose to do it. In all fifty of the United States, there are other alternatives.

Sources:

Fallacy: Black-or-White Fallacy

Technical Note: The type of argument discussed in this entry is not exactly DS, because the first premiss is not quite a disjunction. Rather, the first premiss is a disjunction within the scope of the deontic modality "should". Instead of DS, the argument is a similar form of argument in deontic logic, which is the logic that deals with normative notions such as "should". Its form is:

  1. You should do either A or B.
  2. You should not do A.
  3. Therefore, you should do B.

It should also be intuitively obvious that this form of deontic disjunctive syllogism is validating, for it is a familiar form of moral reasoning. When we are faced with a moral choice between two courses of action, and we know that we should not choose one, we conclude that we should choose the other.

Similarly, the fallacious version of this argument, when there are more legitimate choices than given in the first premiss, is not exactly the Black-or-White fallacy, but a deontic version of that fallacy. Clearly, the following form of argument is non-validating:

  1. You should do either A or B or C.
  2. You should not do A.
  3. Therefore, you should do B.

If, as I contend, Johnson and Stein―and perhaps others―are legitimate candidates, then the argument that you should vote for one of Clinton or Trump because the other one is so terrible commits the deontic version of the Black-or-White fallacy.

Answers to the Exercises:

  1. Non-equivalent. The relation between the two statements is called "conversion", but A statements are not generally equivalent to their converses. Converting an A statement commits the formal fallacy of Simple Conversion of an A Statement.
  2. Equivalent. The statements are related by contraposition, and O statements are equivalent to their contrapositives.
  3. Equivalent. The statements are converses, and E statements are equivalent to their converses.
  4. Non-equivalent. The statements are contrapositives, and I statements are not generally equivalent to their contrapositives.

Solution to a Puzzle for Thanksgiving: Yes, I should bake a ham.

There are many ways to solve this puzzle, but here's one. The third rule tells us that there are two possible cases: either Aunt Alice attends or Uncle Bert does. Let's look at what happens in each case.

  1. Assume that Aunt Alice comes to the dinner. Then, by the first rule, Cousin Carl will refuse to attend. So, by the second rule, I'll either roast a turkey or bake a ham. From the last rule, I'll roast a turkey if and only if Carl does come. Since Carl won't be coming, it follows that I won't roast a turkey. Therefore, I will need to bake a ham.
  2. Now, suppose that Uncle Bert attends the celebration. Then, by the fourth rule, I will serve both fish and ham.

So, whether Alice or Bert comes, I will have to bake a ham.

Technical Appendix: For those familiar with propositional logic, here's a translation of the puzzle together with a proof of the solution using the following dictionary:

A: Aunt Alice comes to the dinner.
B: Uncle Bert comes.
C: Cousin Carl comes.
D: I roast a turkey.
E: I bake a ham.
F: I serve fish.

Using these abbreviations, here is a symbolization of the five rules in standard propositional logic notation:

  1. (A v ~B) → ~C
  2. ~C → (D v E)
  3. ~A → B
  4. B → (F & E)
  5. (A v F) → (D ≡ C)

The conclusion we're aiming for is, of course, E. Let's suppose that E is false for a reductio ad absurdum, that is, assume: ~E.

  1. ~(F & E), from the reductio assumption.
  2. ~B, from 4 and 6 by Modus Tollens (M. T.).
  3. (A v ~B), from 7 by Addition (Add.).
  4. ~C, from 1 and 8 by Modus Ponens (M. P.).
  5. (D v E), from 2 and 9 by M. P.
  6. D, from 10 and reductio assumption by Disjunctive Syllogism.
  7. A, from 3 and 7 by M. T. and Double Negation.
  8. A v F, from 12 by Add.
  9. D ≡ C, from 5 and 13 by M. P.
  10. C, from 11 and 14, which contradicts step 9, so the proof is finished.

Previous Month | RSS/XML | Current | Next Month