
Previous Month | RSS/XML | Current
WEBLOG
November 27th, 2025 (Permalink)
Thanksgiving with the Blancs
Mrs. Blanc had once again1 agreed to host a family Thanksgiving dinner this year and to cook the meal herself. How much food did she need to prepare? She had invited the following Blanc family members: a husband, a wife, a grandfather, a grandmother, two fathers, two mothers, four children, two grandchildren, two siblings, one brother, one sister, two sons, two daughters, one father-in-law, one mother-in-law, one son-in-law, and one daughter in law―Mrs. Blanc herself is included in this list. 26 family members!2
Assuming that all of the invitees attend, what is the minimum number of people―including the hostess―who will need to be fed?
Some invitees are counted more than once. For instance, a brother is also a sibling.
Six
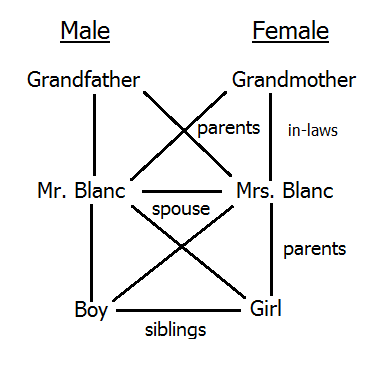
Explanation: We are told that there are four children at the dinner party, so there are at least four attendees, but we're also told that there are a grandfather and grandmother, as well as a father and mother. No one can be both a grandparent and parent of the same person, so for every grandparent, there must be at least two others, one a child and the other a grandchild. Since there are two sons and two daughters, there must be six at a minimum: two grandparents, two children, and two grandchildren.
It's possible that you may have come up with a different family tree that satisfies the relationships in the puzzle. However, I think six family members is minimal unless you engage in a trick such as that in the song "I'm My Own Grandpa"3, in which the narrator is actually his own step-grandfather―that's cheating. You might be able to get the number down to one if time travel were possible4, but science fiction is out.
- ↑Previous Thanksgiving puzzles at the Blanc house:
- A Puzzle to be Thankful For, 11/23/2023
- Thanksgiving Chez Blanc, 11/28/2024
- ↑ When family members are described by a family relationship it means that they bear that relation to some other family member at the dinner party. So, a "son" is not just any male family member, but is the male child of another attendee.
- ↑ For the lyrics, see: Dwight Latham & Moe Jaffe, "I'm My Own Grandpa", The Demented Music Database, accessed: 11/26/2025. This song has been covered by everybody and his grandpa, including the Muppets, but I like this version: "I'm My Own Grandpa", The Stupids, accessed: 11/26/2025.
- ↑ See: Robert A. Heinlein, "All You Zombies", (1959).
November 22nd, 2025 (Permalink)
Untangle the Nots1
Here's a quote from a book on quotations by Paul F. Boller, Jr.:
…Admiral Lewis Strauss…chose…to quote Dr. William Neuman…cautiously warning against continued [nuclear] testing: "Our ignorance in this field is so great that we cannot say with any certainty that we have not already put so much strontium-90 into the stratosphere that harmful fall-out is not inevitable."2
Since nuclear testing is back in the news3, this quotation is accidentally topical, but what does it mean? Boller calls it a "triple-negatively worded statement", but I'm not sure how he arrived at the number three, since I count four negations, highlighted above: "-not" on the end of "cannot", "not", "not" again, and "in-" on the front of "inevitable". Given its complex structure and many negations, Neuman's statement is difficult to understand. Boller goes on to say that Neuman was "suggesting danger from nuclear tests", but is that right?
If you'd like to have a go at untangling Neuman's statement, stop here and do so. Click on the button below to see my analysis.
Let's start out by analyzing the overall structure of Neuman's statement. It's hard to understand partly because it has an internal sentence wrapped within two modifiers. Let's call this internal sentence "S1":
S1: We have not already put so much strontium-90 (Sr-904) into the stratosphere that harmful fall-out is not inevitable.
So, the entire statement can be abbreviated:
Our ignorance in this field is so great that we cannot say with any certainty that S1.
The two sentence modifiers are the phrases "our ignorance in this field is so great that" and "we cannot say with any certainty that". The second of these modifiers directly modifies S1:
S2: We cannot say with any certainty that S1.
S2 tells us that we can't be sure S1 is true. The other modifier modifies S2:
S3: Our ignorance in this field is so great that S2.
S3 is actually Neuman's full statement, and it explains why S2 is true, that is, it explains why we can't say S1 with any certainty. The reason we can't be sure about S1 is that we're too ignorant about the effects of nuclear testing. Neuman would have been more understandable if he'd made this proviso into a separate claim and eliminated the first negation. For instance:
It's hard to be sure that we have not already put so much Sr-90 into the stratosphere that harmful fall-out is not inevitable. This is because our ignorance in this field is so great.
So, let's unwrap S3 by removing the outer modifier and turn to S2. The remaining inner modifier simply says that it's hard to be sure about S1, but what is hard to be sure about? We've eliminated one negation by paraphrasing it away but three remain. Can we get rid of any more?
The most obvious simplification that can be made to S1 is to remove the double negation at its end―"not inevitable". To say that something is "not inevitable" is to say that it is "evitable", which is a real if uncommon English word meaning "avoidable"5. Therefore, we can simplify S1 to:
S1': We have not already put so much Sr-90 into the stratosphere that harmful fall-out is evitable.
However, it is likely, given Boller's report of what Neuman meant, that he should have written:
We have already put so much strontium-90 into the stratosphere that harmful fall-out is inevitable.
Even though both sentences have only a single negation, they do not mean the same thing. Compare the following two sentences:
- The turkey has not already been so long in the oven that burning is avoidable.
- The turkey has already been so long in the oven that burning is unavoidable.
Sentence 1 is denying that the turkey has been so long in the oven that burning is avoidable, which implies that if it were left longer in the oven burning would be avoidable. However, the longer the turkey is in the oven the more likely it is to burn6. So, sentence 1 implies something false. Sentence 2, in contrast, says something sensible, namely, that the turkey has been in the oven too long and burning can no longer be avoided.
Similarly, Neuman was apparently questioning whether nuclear testing had already put so much Sr-90 into the atmosphere that fallout couldn't be avoided. Therefore, he should have said something similar to the following:
We know so little that it's hard to be certain, but we may have already put so much Sr-90 into the atmosphere that fallout is unavoidable.
This has only one negation and it's perfectly understandable if a little wordy.
It appears that Neuman got so tangled up in his own modifiers and negations that he said something he didn't mean. This is why you should avoid using too many negations as you will not only confuse your readers, but you may also confuse yourself.
Notes:
- ↑ Previous entries in this series:
- Untie the Nots, 1/22/2005
- Untie the Nots, Part 2, 2/1/2005
- Untie the Nots, Part 3, 2/1/2010
- Untie the Nots, Part 4, 3/2/2010
- Untie the Nots, Part 5, 2/11/2013
- Untie the Nots, Part 6, 10/1/2013
- Can You Untie the Nots?, 3/24/2016
- Untying the Nots, 11/14/2022
- ↑ Paul F. Boller, Jr., Quotemanship: The Use and Abuse of Quotations for Polemical and Other Purposes (1967), p. 44.
- ↑ Hollie Silverman, "Donald Trump Orders Nuclear Weapons Testing: What To Know", Newsweek, 10/31/2025.
- ↑ "Radionuclide Basics: Strontium-90", Environmental Protection Agency, 2/6/2025.
- ↑ "Evitable", Cambridge Dictionary, accessed: 11/21/2025.
- ↑ At least if the oven is on at a temperature appropriate for cooking turkeys.
November 13th, 2025 (Revised: 11/15/2025) (Permalink)
How to Lie With Notes 21: Latin Abbreviations
Recent codifiers of scholarly usage tend to prefer repeating the short title2 to any use of the Latin abbreviations, and indeed there are indications that the whole apparatus is being simplified as well as Anglicized. But since thousands of books use the older systems dating back as far as the seventeenth century, it behooves the researcher to learn the classic symbols and usages.3
While not as common as they once were, abbreviations of Latin words and phrases still occur in the notes to some scholarly works. Moreover, such notes are ubiquitous in works from previous centuries. In order to detect misleading notes, you have to first understand what the notes mean.
Why Latin? For the same reason that people still wear those silly black robes and square hats during a graduation ceremony: tradition. No one now wears a gown and mortarboard outside of graduation, but in the middle ages it was standard scholarly attire4. To don this garb at graduation is to announce that you are now a scholar who is a part of a tradition stretching back many centuries to a time when people dressed funny5.
Latin used to be the language of scholarship, so that scholars who spoke different native languages could communicate in a common scholarly tongue. Today, that language is no longer Latin, but English, which is one reason why Latin in notes is diminishing if not disappearing entirely.
Why are the Latin words and phrases used in notes abbreviated? It's not to make them more mysterious, though it may have that effect, but to make them more compact so as to take up less space at the foot of the page―endnotes can afford to be more expansive. For the same reason, footnotes are often printed in a smaller font than the text, which can make them difficult to read. In notes, space is precious.
Here are the most common abbreviations, not in alphabetical order but roughly in frequency of occurrence and importance to understand:
- Ibid.: This is the most common Latin abbreviation you are likely to come across in notes to works with any scholarly pretension. "Ibid." is short for "ibidem", an adverb that means "in the same place" or "at the same time"6. Its literal meaning helps a little to understand but doesn't fully explain how it's used in notes. When "ibid." occurs in a note, it refers back to the previous note, so that an entire citation doesn't need to be repeated7. If the reference is to the same page or pages as the previous note, then "ibid." alone can do the job. For instance, footnote 9 of chapter 3 in The Modern Researcher is simply "Ibid."8 The previous footnote on the same page reads:
8 Quoted in W. K. Hancock, Country and Calling, London, 1954, 95.9
This says that the quote in the text on the same page that is followed by a superscript "8" is from page 95 of the book Country and Calling by W. K. Hancock, which was published in London in 1954. So, the subsequent quote, followed by a superscript "9", is from the same page of the same book.
The purpose of "ibid." is to save the scholar and the reader from repeating the same citation as given in the previous note, but what do you do when you want to cite a work you've already cited but not in the immediately preceding note? That's where our next abbreviation comes in:
- Op. cit.: "Op. cit." is an abbreviation of "opere citato", which means "in the work cited"10. This does the same job as "ibid." except that it jumps over the previous note. If only one work has been so far cited, or only one by the author mentioned in the noted text, then "op. cit." is used followed by the relevant page number(s). For instance, in Charles Stevenson's Ethics and Language, we find the note: "23. Op. cit., p. 268."11 The note refers back to the following note from a few pages earlier:
16. Methods of Ethics (Macmillan, 1874).…12
We can tell that this is the relevant work because the author, Henry Sidgwick, is mentioned in the text in both places. If multiple authors have already been noted, then "op. cit." would need to be preceded by the author's last name in order to indicate which work is cited.
- Loc. cit.: "Loc. cit." is short for "loco citato", which does not mean "crazy citation" but "in the location cited"13. "Loc. cit." is just "op. cit." when the note refers back not only to the work cited, but to the same page(s), that is, the same "location". For instance, Thomas Kuhn's The Structure of Scientific Revolutions has the following footnote:
6 Albert Einstein, "Autobiographical Note," in Albert Einstein: Philosopher-Scientist, ed. P. A. Schilpp (Evanston, Ill., 1949), p. 45.14
This tells us that the quote of Einstein on the same page comes from page 45 of Albert Einstein: Philosopher-Scientist, edited by P. A. Schilpp, and published in Evanston, Illinois in 1949. Several pages later, we see the note:
14 Einstein, loc. cit.15
This indicates that the claim followed by a superscript "14" on the same page comes from the same book and page as the previously cited quote from Einstein.
Robert J. Gula wrote forty-five years ago about "loc. cit." that: "This abbreviation used to be used in footnotes but has recently been replaced by ibid., or by the author's last name followed by the first words of the title [that is, the "short title"]."16 As mentioned above, "op. cit." is sometimes used this way, so "loc. cit." can be dispensed with, but you still may come across it, especially in older works such as Kuhn's.
- pass.: "Pass." abbreviates "passim", which is often spelled out in full, and means "here and there".17 It refers to a reference that occurs "here and there" or scattered throughout the work cited, and is used when there are too many pages to cite individually. For instance, another note of Stevenson's reads in part:
30. … An instructive study of metaphor has been made by I. A. Richards,… Interpretation in Teaching (Harcourt, Brace, 1938), passim. … 18
This means that the "instructive study of metaphor" is found here and there throughout the book cited.
- cf.: This abbreviates the Latin word "confer", which means "compare"19, and it's occasionally found in notes preceding a citation to a work that the writer suggests be compared with the claim noted. Stevenson makes frequent use of it in footnotes20.
- f. & ff.: A single "f." abbreviates the Latin word "folio" for a page or leaf in a book21. Instead of writing, say, "pp. 123-124", "pp. 123f." means the same thing, that is, "page 123 and the following page". The double "f" in "ff." is like the double "p" in "pp.", that is, it means "pages following", so that "pp. 32ff." means "page 32 and the pages following". The double "f" indicates at least two pages following, but it could be more.
- idem: "Idem", sometimes abbreviated "id.", means "the same"22 and is used to avoid repeating a name, title, or reference from the preceding note. As a result, "idem" can be used in the same way as "ibidem", above, and Stevenson seems to use it exclusively instead of "ibid."23.
Those are the most common Latin abbreviations used in notes that don't also occur in the text itself, or in other contexts. In the next installment, we'll anatomize the structure of a citation.
Notes:
- ↑ Part one is here: How to Lie With Notes: Introduction, 10/23/2025.
- ↑ By the "short title", Barzun & Graff mean a shortened version of the full title of a scholarly work. For instance, they refer to Charles A. Beard's An Economic Interpretation of the Constitution by the short title "Economic Interpretation", see: Jacques Barzun & Henry F. Graff, The Modern Researcher (1977), pp. 267 & 286-287.
- ↑ Ibid., p. 286.
- ↑ For the history of the academic cap and gown, see: Jonathan Rapoport, "Pomp and Circumstance", Slate, 6/11/2010.
- ↑ This is not to say that people don't dress funny nowadays.
- ↑ Eugene Ehrlich, Amo, Amas, Amat and More: How to Use Latin to Your Own Advantage and to the Astonishment of Others (1985).
- ↑ Barzun & Graff, loc. cit.
- ↑ Ibid., p. 42.
- ↑ Ibid.
- ↑ Ehrlich, op. cit.
- ↑ 1965, p. 223.
- ↑ Ibid., p. 219.
- ↑ Ehrlich, op. cit.
- ↑ 3rd edition, 1996, p. 83.
- ↑ Ibid., p. 89.
- ↑ Robert J. Gula, Precision: A Reference Handbook for Writers (1980), p. 250.
- ↑ Jon R. Stone, Latin for the Illiterati (1996).
- ↑ Op. cit., p. 76.
- ↑ Stone, op. cit., p. 21.
- ↑ Op. cit., passim.
- ↑ Brewer's Dictionary of Phrase & Fable, edited by Ivor H. Evans (Centenary edition, 1981).
- ↑ Ehrlich, op. cit.
- ↑ Op. cit., passim.

November 1st, 2025 (Permalink)
The End of Nature
Anna Krylov, "Why I no longer engage with Nature publishing group", Heterodox STEM, 10/24/2025
…Scientific publishers play a key role in the production of knowledge…. The role of the publisher is to be an epistemic funnel: it accepts claims to truth at one end, but permits only those that withstand organized scrutiny to emerge from the other, a function traditionally performed by a rigorous peer-review and editorial process. This process should be guided by scientific rigor and a commitment to finding objective truth.Unfortunately, the Nature group has abandoned its mission in favor of advancing a social justice agenda. The group has institutionalized censorship, implemented policies that have sacrificed merit in favor of identity-based criteria, and injected social engineering into its author guidelines and publishing process. The result is that papers published in Nature journals can no longer be regarded as rigorous science. Three representative examples illustrate this decline:
- Institutionalized social engineering
The Springer Nature Diversity Commitment…openly pledges to "take action to improve diversity and inclusion in the conferences we organise, and in our commissioned content, the peer review population and editorial boards." Editors are "asked to intentionally and proactively reach out to women researchers" and authors are instructed to suggest reviewers "with diversity in mind." In other words, editorial choices and peer review are to be guided not solely by competence but by demographic attributes. …
- Ideological subversion of literature citations
Nature Reviews Psychology…now encourages authors to practice "citation justice"―that is, to social-engineer their manuscript's bibliography to promote members of favored identity groups, even if their works lack the requisite merit or relevance. "Citation justice" is particularly harmful because it undermines the rigor and reliability of published research. When references are chosen not for their scientific relevance or quality but to promote the work of preferred identity groups, the integrity of science itself is compromised….
- Institutionalized censorship
Nature Human Behavior has published a censorship manifesto…now widely criticized…in which they openly declare their intent to censor legitimate research findings that they deem potentially "harmful" to certain groups. Not only is it arrogant for editors to presume they have the expertise to make such judgments, the practice is antithetical to the production of knowledge.
Any of these policies, taken alone, would undermine the epistemic standards of scientific publishing as a pillar of the truth-seeking enterprise. Together they represent a profound corruption of purpose. The purpose of science is the pursuit of truth, not the advancement of diversity, equity, and inclusion. These examples disturbingly reveal that scientific publishing at Nature has become ideologically corrupt.
Disclaimer: I don't necessarily agree with everything in this article, but I think it's worth reading in its entirety. In editing the excerpt, I sometimes changed the paragraphing.

October 31st, 2025 (Permalink)
Hallowe'en Party
Andy, Betty, Charly, and Debby attended a party on Hallowe'en costumed as a mummy, a vampire, a werewolf, and a ghost, though not necessarily in that order. At the end of the party, there was a best costume contest that each of the four friends entered. As a result, each of the four costumes was ranked from best to worst. Given the following clues, can you figure out what costume each friend wore?
- The contestant in the werewolf costume didn't do as well as the one dressed as a vampire, but didn't come in last among the four friends.
- Andy didn't come out ahead of Betty in the contest, and there was at least one other contestant between them in the ranking.
- The entrant wrapped up in gauze like a mummy came out better in the contest than the one made up as a werewolf, though there was no other contestant between them.
- Debby just barely beat out Charly, who had the next best costume.
What costume was worn by each contestant and in what position did each finish?
Betty was first in the contest wearing the vampire costume; Debby came in second wrapped up like a mummy; Charly, made up as a werewolf, came in third; and, finally, Andy was dead last as a ghost.
October 23rd, 2025 (Permalink)
How to Lie With Notes1: Introduction
This is the first entry in what I hope will be a series of entries on the misuse of notes―that is, footnotes or endnotes―in scholarly or pseudo-scholarly writing.
When I first started reading scholarly works, many decades ago, I recall being baffled by the notes. Some typical notes looked like the following:
14 Ibid.
18 Sutch, op. cit., 429.
19 New York, 1938.2
I recall struggling to understand this arcane language of scholars. It's bad enough that some notes included words taken from a dead language―Latin―but they were abbreviated as well. Moreover, scholarly notes were taught by the "sink or swim" method: you were thrown into the deep end of scholarship and either learned quickly to swim or drowned3.
Scholarly notes, whether at the foot of a page―"footnotes"―or the end of an article, chapter, or book―"endnotes"―are not just pedantry. If used correctly, notes serve useful purposes, but if used incorrectly they can mislead the reader. To understand how notes are misused, we must first understand how they are properly used.
What are notes for? Notes serve more than one purpose, in fact, they have three main uses:
- Citation of sources: Notes of this type cite books or other sources of a scholarly work's claims, which serves the important purpose of making it possible for readers to check those claims. For instance, suppose that a work quotes from another work: how do we know that the other work is not misquoted or quoted out of context? A citation in a note to the work and page or pages quoted means that the quote can be checked for accuracy as well as contextomy. Even if no one ever does so, the fact that the note makes it possible serves as a deterent to conduct unbecoming a scholar. If you're more likely to get caught, you're less likely to cheat. Here's an example of a note of this type:
1 Austen H. Layard, Discoveries in the Ruins of Nineveh and Babylon… London, 1853, 663.4
This footnote is a citation to the source of a lengthy quote included on the same page. The note gives, first, the author's name, then the title of the book, the place and year of publication and, finally, the number of the page where the quote occurs. The ellipsis after the title indicates that the full, lengthy nineteenth-century title has been truncated5.
- Asides and digressions: It's a common and laudable practice to put into notes comments that would break the flow of argument and that a reader could skip without misunderstanding the main points. Such comments can, especially if short, be included in the text in parentheses, but long parenthetical remarks interrupt the reader's train of thought. It's better to exile such remarks to the foot of the page or the end of the book. For example, a logic textbook I own gives an example of modus ponens6 from one of A. A. Milne's books7 and footnotes it as follows:
22 And to think that Eeyore always maintained that Pooh had only fluff in his head!8
This is an amusing aside that will only be understood by readers familiar with Winnie the Pooh, otherwise adding nothing to the discussion of the example.
- Technical elaborations or provisos: These are similar to the digressions and asides of the previous point, but the reason for putting them into a note is different. In this case, the writer places material too technical for many readers, but which more advanced readers may want to read. For instance, the same textbook from which the previous example came remarks in its "Preface to the Instructor": "Where the textual explanation warrants a special comment or remark to advanced readers but students need not read the same comment, or a footnote presupposes special technical background, it is labeled 'Note to Advanced Readers.'"9
It should be noted that these three categories are not exclusive, and perhaps not exhaustive. Some notes combine two of these categories, and it's even possible that a single note could combine all three.
What these three types have in common is that they are written matter that the casual reader may skip without missing anything important to the main discussion. The notes are there for those who want to check sources―type 1―advanced readers who want technical information―type 3―or those who just wish to enjoy an amusing or interesting sidelight―type 2.
If all goes as planned, next month we'll take a brief look at the Latin phrases and abbreviations that have been traditionally used in notes. After that, we'll get into the ways that notes go bad.
Exercise: Test your understanding by classifying the following notes according to the three types above. Keep in mind that a note may be of more than one type and there may be borderline cases.
- Type 2
- Type 1
- Type 2
- Types 1 & 2
- Type 2
- Type 3
- Type 1
- Type 1
- Type 1
Notes:
- ↑ And without.
- ↑ Jacques Barzun & Henry F. Graff, The Modern Researcher (3rd edition, 1977), pp. 29, 184 & 293.
- ↑ The best brief introduction to scholarly notes that I know of is: ibid., chapter 15. Unfortunately, I didn't read this chapter until many years later.
- ↑ Barzun & Graff, p. 3. The fact that I simply cite the last names of the authors and a page number indicates that I've previously given the full citation in note 1, above.
- ↑ The full title is: Discoveries Among the Ruins of Nineveh and Babylon; with Travels in Armenia, Kurdistan, and the Desert: Being the Result of a Second Expedition Undertaken for the Trustees of the British Museum. No wonder it was abbreviated!
- ↑ Modus ponens is a type of argument from propositional logic that has the form: If p then q, p; therefore, q.
- ↑ A. A. Milne, The House at Pooh Corner (1928).
- ↑ Stephen Naylor Thomas, Practical Reasoning in Natural Language (4th edition, 1997), p. 219.
- ↑ Ibid., p. xiii.