WEBLOG
Previous Month | RSS/XML | Current | Next Month
March 30th, 2013 (Permalink)
Headline
One-armed man applauds the kindness of strangers
The sound of one hand clapping.
Source: "20 (Un)intentionally funny news headlines", Banned in Hollywood, 1/19/2012
March 24th, 2013 (Permalink)
Fact Check it Out
Longtime readers of this weblog may remember Spinsanity, which was the best and most objective of the media watchdog sites several years ago, and whose stories I often pointed readers to. Brendan Nyhan, who was one of the three watchdogs of that site, has an article in the Columbia Journalism Review about factchecker Glenn Kessler turning into a pundit. I've criticized the tendency of factchecking to turn into punditry myself (see the Resource, below), but I do have a quibble with the following comment:
Factchecking is an inherently subjective enterprise; the divide between fact and opinion is often messy and difficult to parse. …it is therefore essential that factcheckers like Kessler only invoke the authority of facts when assessing claims that can be resolved on evidentiary grounds, rather than straying into subjective judgments about the political process or semantic debates over terminology.
I don't know why Nyhan says that factchecking is "inherently subjective", since he seems to contradict himself in his subsequent excellent advice to factcheckers to avoid "straying into subjective judgments". If it's possible for a factchecker to avoid such judgments, then factchecking must not be inherently subjective.
I agree with Nyhan that the distinction between fact and opinion is "messy and difficult to parse" or, more precisely parsed, it is vague. However, that vagueness does not make it inherently subjective any more than the vagueness of the concept of baldness makes it subjective whether Patrick Stewart is bald.
There are borderline cases of baldness―that's what makes it vague―and one might say that it's "subjective" whether such a borderline case is bald. However, there are also clear-cut cases of baldness―such as Patrick Stewart―as well as uncontroversially non-bald people, while the borderline cases fall in a grey zone in-between. Similarly, there is a grey zone between fact and opinion, but some things are clearly factual and others clearly matters of opinion. Factcheckers should strive to stay well within the factual zone, and outside the grey zone.
Source: Brendan Nyhan, "Thatís not a factcheck! ", Columbia Journalism Review, 3/12/2013
Resource: Fact Checkers are Sacred, 1/5/2012
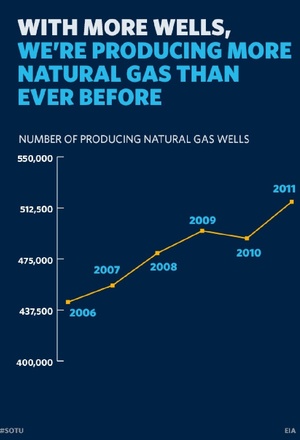
March 21st, 2013 (Permalink)
Charts & Graphs: The Gee-Whiz Line Graph
Since I've recently begun posting examples of misleading charts and graphs, this is the first entry in a short series on the most common ways in which such graphics can mislead. Take a look at the line graph to your right, which is taken from the President's enhanced State of the Union address from earlier this year (see Source 1, below). Gee whiz! The number of natural gas wells is sure shooting up!
However, if you take a close look at the scale on the left of the graph, you'll see that it begins at 400,000 and ends at 550,000, which is a span of 150,000 wells, and the growth in number of wells is about half that. So, the number of wells has increased around 15% in the five years shown on the graph. This is a substantial increase, but not as impressive as a quick glance at the graph suggests.
I call this type of line graph a "gee-whiz graph", after the title of the chapter in Darrell Huff's How to Lie with Statistics where he discusses it. Also, it's a common enough kind of graph that it could use a name, and I don't know of another. It's a fairly good name, too, since the main use of graphs of this type is to visually exaggerate an increase, or decrease, thus causing the "gee whiz" reaction. This is done by stretching the vertical scale in order to make an increase or decline steeper, and then often truncating it―as was done with our example―so that the change takes up a larger portion of the graph. For instance, the increase in the example takes up about half of the graph, which could give the impression, if you didn't pay close attention to the scale, that the number of wells has approximately tripled.
In contrast, if we wish to visually diminish the size of a change, we can simply do the reverse: start the scale at zero and squash it, as in the second graph at right (adapted from one taken from Source 3, below). The result is more of a ho-hum graph, given that the small apparent change is not likely to cause a strong reaction, but it shows the same information as the gee-whiz one.
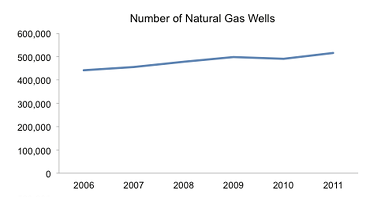
Now, there's no law against putting charts and graphs on the rack and stretching them, nor cutting off their bottoms to fit a Procrustean bed. One possible rationale for torturing the graph in this way (suggested in Source 3, below) would be to highlight the year-to-year changes in the number of wells, which are nearly impossible to see in the ho-hum graph because its line is nearly straight. However, why would the White House, which produced the graph, want to draw attention to the fact that the number of wells actually declined from 2009 to 2010, which was the President's first year in office? More likely, the White House was going for the "gee whiz" reaction.
So, the moral of our first lesson is to always pay close attention to the vertical scale of a line graph: Does it start at zero? If not, why not? Has the scale been stretched or squashed, and if so is there a good reason why? If you can ask and answer these questions, your "gee whiz" may just turn into a "ho hum".
Sources:
- "Enhanced State of the Union", The White House, 2/12/2013
- Darrell Huff, How to Lie with Statistics (1954), Chapter 5: "The Gee-Whiz Graph"
- NPR Staff, "Chart Check: Did Obama's Graphics 'Enhance' His Big Speech?", NPR, 2/14/2013
March 18th, 2013 (Permalink)
New Book: All Natural
I came across this intriguing new book today which claims in its subtitle to be "a skeptic's quest to discover if the natural approach to diet, childbirth, healing, and the environment really keeps us healthier and happier". I haven't read the book yet, but I'm rather skeptical about just how much of a skeptic the author, Nathanael Johnson, really is. The book is published by Rodale, which also publishes Organic Gardening Magazine, as well as such books as 100 Natural Remedies for Your Child, Eco-Beautiful: The Ultimate Guide to Natural Beauty and Wellness, and The Green Pharmacy Guide to Healing Foods: Proven Natural Remedies to Treat and Prevent More Than 80 Common Health Concerns. So, it seems doubtful that Rodale would choose to publish a book that was very skeptical of natural remedies, but if so then good for them. However, if it's the only skeptical book they've published then it's greatly outnumbered by the non-skeptical ones.
It appears that everyone today is calling themselves a "skeptic", including conspiracy theorists. I suppose that this is a testament to the success of skepticism in that everybody wants to jump on the bandwagon, but it has the effect that the word no longer has much meaning. Nonetheless, if the book turns out not to be very skeptical, it may be of interest as a source of examples of fallacies―especially the appeal to nature, of course. It might even end up on the Fallacy Files' Shelf of Shame between The Abortion Holocaust and The Secret.
Source: Nathanael Johnson, All Natural*: *A Skeptic's Quest to Discover If the Natural Approach to Diet, Childbirth, Healing, and the Environment Really Keeps Us Healthier and Happier (Rodale: 2013)
Fallacy: Appeal to Nature
March 17th, 2013 (Permalink)
Check it Out
Volokh conspirator Ilya Somin has an interesting post (see Source 2, below) in response to one from the economist David Friedman (see Source 1, below) on the important problem of when to defer to the consensus of expert scientific opinion.
I agree with Friedman that there are likely to be efforts made by interest groups to capture scientific bodies that pass public judgments on issues of political interest, and these efforts may have some success. However, what he doesn't mention is that such bodies have a countervailing interest in not becoming politicized, because of potential damage done to their reputations. So, one thing that we non-experts can do in deciding whether such a group represents a consensus of experts is to examine its reputation, and you don't need to be an expert to do that.
Friedman suggests that, given the problem of politicization of scientific bodies, we should examine the evidence for ourselves rather than defer to the consensus of experts. However, Somin is right that this is seldom realistic. If you're an expert then you're entitled to your opinion, even if you're a minority of one. If you're not an expert but will devote the time and effort necessary to understand a scientific question well enough to have an informed opinion, good for you. But this does not mean a few minutes at the "University of Google"―that's how we get pseudo-experts such as Jenny McCarthy. Scientific issues may require years of study in order to develop sufficient expertise to form an opinion, and in the meantime you'll have to fall back on the consensus of experts.
So, what should we do if we don't have the time, money, or energy to become experts on a scientific subject ourselves? If possible, we can suspend judgment, which is why you won't find me opining here about climate change: I'm not an expert and I don't have an opinion about that. However, sometimes we have to form an opinion about scientific matters outside our area of expertise, especially when―like climate change―they have political consequences. This is where Somin's rules of thumb may come in handy.
Sources:
- David Friedman, "Official Scientific Truth ", Ideas, 3/5/2013
- Ilya Somin, "Science, Political Ignorance, and Deference to 'Authoritative' Experts", The Volokh Conspiracy, 3/6/2013
March 13th, 2013 (Permalink)
Math Test
Try the following two math problems:
- 6 ÷ 2(1 + 2) = ?
- 48 ÷ 2(9 + 3) = ?
Can you solve these equations?
March 2nd, 2013 (Permalink)
The Last Puzzling List
Suppose that you find a piece of paper with the following list of sentences printed on one side:
- At least one of the statements on this list is false.
- At least two of the statements on this list are false.
- At least three of the statements on this list are false.
- At least four of the statements on this list are false.
- At least five of the statements on…
At this point, the piece of paper has been torn across and the bottom is missing. Let's assume that the list goes on in this fashion, but that you can't tell exactly how many sentences are on the list. However, let's also assume that there are an odd number of sentences on the list. Call the last sentence on the list "n", where n is an odd number. So, sentence n would read:
n. At least n of the statements on this list are false.
Also, let's assume that each of the n sentences on this list is either true or false. Can you determine how many of them, if any, are false? How many sentences, if any, are true? Which sentences are true and which false?
Resources:
- A Third Puzzling List, 11/7/2012
- A Fourth Puzzling List, 12/1/2012
- A New Puzzling List for a New Year, 1/1/2013
- 9 or 1
- 288 or 2
The two equations are ambiguous, and which of the two possible answers you come up with will depend upon what grouping convention, if any, you use. The usual convention for order of operations is to do anything in parentheses first, then multiply and divide, and finally add and subtract. This, however, won't tell you what to do when there's more than one addition/subtraction, or multiplication/division, in an equation. An additional convention is to work from left to right, so that if you have to multiply/divide, or add/subtract more than once, you start from the leftmost operation and work to the right. If you follow this convention, then the correct answer to each equation will be the first one given above. This complete set of conventions is sometimes labelled with the mnemonic "PEMDAS"―see the Sources, below, if you're interested―which is an acronym for "Parentheses, Exponentiation, Multiplication, Division, Addition, Subtraction".
If instead of working from left-to-right you multiply before dividing, you will get the second answer to both equations. This answer is not "wrong" unless the left-to-right convention has been adopted, and you'll notice that I wrote nothing about any ordering conventions in stating the problems.
I'm not sure when and where PEMDAS was widely adopted, but it appears that it was sometime in the last half-century or so, at least in the United States. I don't recall learning it as a child, but perhaps that's just because that was so long ago. However, Americans who are middle-aged or older may not have learned it.
Moreover, even those who at some point learned the acronym and still remember it, may well misinterpret it to mean that multiplication should be done before division, since "M" occurs before "D" in "PEMDAS". This qualifies as a mistake though a natural one.
In addition, though I'm not sure it rises to the level of a convention, there's a tendency to treat implicit multiplication―that is, multiplication indicated by adjoining two symbols without a multiplication sign―as taking precedence over explicit division. This is what I did when I first came across these equations elsewhere.
Sources:
- "History of the Order of Operations", Ask Dr. Math, 11/22/2000
- George Mark Bergman, "Order of arithmetic operations; in particular, the 48/2(9+3) question."
- Tara Haelle, "What Is the Answer to That Stupid Math Problem on Facebook?", Slate, 3/12/2013
Solution to the Last Puzzling List: If you've been following along through these puzzling lists, you may recognize this one as a generalization of the previous list. That list turned out to be paradoxical, so you might correctly guess that this one also will be paradoxical. However, how can you prove that this list is paradoxical? We were able to do that with the other list because it was short and we could check each distribution of truth-values to see that none were possible. However, in this case we don't even know exactly how long the list is; all that we know for sure is that there are an odd number of entries on the list.
First of all, it's easy to see that the members of the list cannot all be one truth-value: They can't be all false, since if the first sentence were false then all of them would have to be true; but they can't be all true, since each of them says that at least some are false. Therefore, we know that some of the sentences will be true and some false.
In solving the previous list, we saw that the truth of any given sentence on such a list implies the truth of all previous sentences. Therefore, the true sentences must constitute an initial sequence of the list. We don't know how long this sequence of true sentences is, but let's call its length "k". So, k sentences on the list are true, which means that the first sentence is true, the second sentence is true, … the kth sentence is true. Therefore, at least k sentences on the list are false, since that's what the kth sentence says.
Because the last sentence in the sequence of true sentences is sentence k, sentence k+1 is the first false sentence on the list. Here's what k+1 says:
k+1. At least k+1 of the statements on this list are false.
Since sentence k+1 is false, that means that it's not true that at least k+1 of the sentences are false. So, no more than k of the sentences can be false. Since we already know that at least k of the sentences are false, it follows that exactly k sentences on the list are false.
However, since there are k true sentences on the list and k false sentences on the list, that means that the list must be 2k sentences long. But 2k is an even number, and we know that the list is an odd number in length. This is a contradiction, which means that our assumption that all of the sentences on the list have a truth-value must be false. Instead, there must be at least one sentence on the list that is neither true nor false.
Personally, I think that none of the sentences on this or any similar list is true or false. Now, I can't prove that none of them has a truth-value; I can only prove that at least one of them is neither true nor false. However, I think that the sentences are so similar that as one goes so go the others. If one lacks a truth-value, then so do they all.