WEBLOG
Previous Month | RSS/XML | Current | Next Month
May 30th, 2013 (Permalink)
Headline
Michelle Obama rewards kids who planted her garden with arugula salad, broccoli pizza
This headline raises many questions: I can see planting arugula or broccoli, but how do you plant salad or pizza? Why would anyone put broccoli on pizza? In what sense is that a reward?

May 28th, 2013 (Permalink)
A Five-Legged Calf
"In discussing the question, [Lincoln] used to liken the case to that of the boy who, when asked how many legs his calf would have if he called its tail a leg, replied, 'Five,' to which the prompt response was made that calling the tail a leg would not make it a leg."
From an article in the Wisconsin State Journal:
ďOur teachers havenít had a raise for the last three years.Ē―Ed Hughes, clerk and candidate for president of the Madison School Board … During teachers union contract negotiations, public school and union officials routinely refer to a ďraiseĒ as something that is distinct from and in addition to the automatic bumps in salary teachers are already getting for remaining on the job and accruing more college credit. … Itís such parsing that allows Hughes to say teachers havenít gotten raises―and to be right, at least in one context. The Madison Schools teacher salary schedule provides increases of between a few hundred dollars to more than a $1,000 for each year of service and in the range of $3,000 to $7,000 more a year for getting a masterís degree. For this school year, 2,498 of 2,700 teachers got salary increases for longevity and degree attainment. Hughes acknowledged that itís probably fairer to define seniority and degree-attainment hikes as raises.
In other words, how many raises would the teachers have received in the last three years if you don't call an automatic yearly salary increase a raise. "None," says Ed Hughes, to which the prompt response should be that not calling a yearly salary increase a raise doesn't mean it isn't one.
Sources:
- "Parent Night!", Funny Signs. I guess the shots are to prepare you for parents' night.
- Allen Thorndike Rice, collector & editor, Reminiscences of Abraham Lincoln by Distinguished Men of His Time (new and revised edition, 1909), p. 242.
- Chris Rickert, "A raise by many other names", Wisconsin State Journal, 4/27/2013.
May 21st, 2013 (Permalink)
Q&A
Q: I was wondering if you have good references about how to counter-argue each fallacy, which I find sometimes very hard, specially because many of them are heuristically valid (although not necessarily). Some are specially hard to argue since the person might not be convinced by a simple announcement that they used a fallacy, I find that a good strategy is to give a plausible counter-example, but sometimes it is very hard to find one quickly.―Leo Arruda
A: I agree that simply announcing that someone has committed a fallacy, or even identifying it by name, is often not an effective way to argue. If you can count on the person committing it not just knowing the name of the fallacy, but understanding it, then perhaps such an announcement might work. However, if someone actually knows this much, he or she likely won't think that his or her argument is fallacious. So, even in the best circumstances, you may need to explain why the argument does commit a fallacy. Of course, to do this you have to understand the fallacy well enough to explain it to someone else, but if you can't do that then you probably shouldn't be making any accusations of fallacy anyway.
The technique of producing a counterexample to a fallacious argument is called "refutation by logical analogy", though T. Edward Damer calls it the "absurd example method" (see the Source, below, pp. 27-29). Such a counterexample is an argument with the same logical form as the fallacious argument one aims to refute, but with obviously true premisses and an uncontroversially false conclusion. Such an argument shows that the logical form shared by the example and the argument to be refuted is non-validating, that is, not every argument of that form is valid since no valid argument has true premisses and a false conclusion.
How do you know whether an analogous argument has the same form as the argument that you wish to refute? Unfortunately, logical form is a technical area of formal logic, and short of learning a lot of logic you'll probably have to rely on your intuitive sense of when two arguments are similar in structure.
A refutation by logical analogy is enough to dispose of any fallacious deductive argument intended to be formally valid, but many logical fallacies involve non-deductive reasoning. A logical analogy cannot refute a fallacious inductive argument since what it shows is that the argument form is non-validating, which we knew already since no inductive argument form is validating―if it were it wouldn't be inductive. For these types of argument, the purpose of the counterexample is to show what's wrong with arguing in the fallacious way. How this works is more a matter of psychology than logic, since the counterexample should simultaneously show why the form of argument is psychologically tempting, but that it can lead one astray. Unfortunately, there's no recipe―or algorithm―for creating a counterexample to such an argument. It takes imagination and it's hard work.
Given all of these difficulties, I think that in discussion or debate it's best to use counterexamples as a way to clarify what someone is arguing. Ask the arguer: "How is your argument different from this one?", and be prepared for the possibility that the arguer will be able to show that the argument in question differs in some relevant way. At the very least, though, if you can produce a logical analogy then the burden of proof is on the arguer to show such a difference.
Finally, I'm not aware of much literature on this subject, but you might take a look at Damer's textbook Attacking Faulty Reasoning. This is a text about logical fallacies, and each fallacy section ends with a subsection titled "Attacking the Fallacy", which explains ways to criticize instances of the fallacy. There's also a general section on how to attack fallacies (chapter 3). However, I haven't seen any editions since the third one, so I don't know whether the later editions continue to include these useful features.
Also, many of the entries in The Fallacy Files, though by no means all, include "CounterExamples", especially those for formal fallacies, which are in fact refutations by logical analogy. You might try to remember some of these for the more common fallacies, or look them up if you can.
Source: T. Edward Damer, Attacking Faulty Reasoning (3rd edition, 1995)
May 17th, 2013 (Permalink)
The Puzzle of the Library Books
Adam, Beth, and their daughter, Cathy, like to visit their local public library to check out books. They always check out either mysteries or puzzle books, but never more than one book apiece. Either Adam or Beth will select a mystery novel. If Adam picks a mystery then Cathy will choose a puzzle book. If Cathy selects a puzzle book then Beth will check out a mystery. Adam and Beth won't both select the same kind of book. Who checked out a mystery on one trip to the library but a puzzle book a different time?
May 15th, 2013 (Permalink)
Headlines
New salt study suggests that U.S. guidelines on sodium are too strict
New salt study shows sodium levels in food still high
These are two current headlines about two different studies that came out at about the same time. Have you ever wondered why you see so many conflicting news reports, such as these, about scientific studies on health and diet? Philosopher Gary Gutting has a worthwhile article explaining this puzzling phenomenon (see the Source, below). Hint: The problem isn't so much with the studies as it is with the reporting. Check it out.
Source: Gary Gutting, "What Do Scientific Studies Show?", The Stone, 4/25/2013
May 13th, 2013 (Corrected: 9/25/2019) (Permalink)
BoP!
Massimo Pigliucci has an interesting article in the most recent issue of Skeptical Inquirer magazine on the notion of the burden of proof (BoP). The onus probandi is probably most familiar from the law where―at least in the U.S.―the onus in a criminal trial is on the prosecution. Pigliucci doesn't mention it, but there is a presumption corresponding to the onus; in criminal law, it is that the defendent is presumed to be innocent. Of course, such a presumption can be overcome, otherwise no one would ever be convicted, but to do so the prosecution must present sufficient evidence of guilt to shift the onus to the defense. Exactly how much evidence and of what kind is necessary to overcome the presumption of innocence is, of course, a legal question that I won't go into since I'm not a lawyer. But, at the very least, placing the onus and presumption where they are means that the prosecution must present some evidence, while the defense needn't present any if the prosecution fails to shoulder its burden.
Outside of the law, is there a presumption corresponding to the BoP? Yes, because this relation is a logical one: to say that there's a burden on those that argue P is to say that there's a presumption that P is false, and to say that there's a presumption that P is true is to say that there's a burden on those that argue not-P. Pigliucci is right that where the BoP lies is not a simple matter of who makes a positive claim; rather, it's determined by the degree of plausibility of the claim. Carl Sagan's famous slogan that "extraordinary claims require extraordinary evidence" is a specific application of the BoP: an "extraordinary claim" is one that is highly implausible because it goes against what we already know, so that the BoP is heavily weighted against it, that is, it requires "extraordinary evidence" to overcome.
So, I like the idea of applying Bayes' Theorem to determine where the load lies and how heavy it is, but I think that Pigliucci makes a mistake in the following sentence: "…[I]f we set our priors to 0 (total skepticism) or 1 (faith), then no amount of evidence will ever move us from our position…". He's certainly right about a prior probability of zero, since that would cause the posterior probability of the hypothesis on the evidence to also be zero. However, setting the prior probability of a hypothesis to one means that the prior drops out of the equation, so that―using Pigliucci's notation―P[T|O] = P[O|T]/P[O]. If P[O|T] = 0, then the posterior probability of the hypothesis would also equal zero. P[O|T] would be equal to zero in case the theory, T, implied that the observation, O, would be false. So, even if we started out with "faith" in the hypothesis, if the hypothesis implies something that turns out to be false then the probability of the hypothesis will drop to zero.
For this reason, I think that it's wrong to call setting the prior probability of a hypothesis to one "faith" in the hypothesis. Rather, faith in a hypothesis would probably manifest itself in refusing to update the prior probability in the face of counter-evidence. In other words, "faith" is a disposition to irrationally cling to a belief in the face of counter-evidence: a person who has "faith" in a particular theory will choose to reject the evidence against it rather than to reject the theory. In contrast, setting a prior probability to zero does involve a kind of closed-mindedness that should be avoided, except in cases where the hypothesis is self-contradictory: in that case, the prior should indeed be set to zero, since there's no possibility that the hypothesis can be true. However, any consistent hypothesis has a non-zero, though perhaps very small, probability of being true. In general, outside of logical truths and falsehoods, no priors should be set to the extreme values of zero or one.
This means that the BoP and its corresponding presumption are not all-or-nothing, as they may seem to be, but matters of degree. For instance, if someone claimed that there was a deer in my backyard, I would take that person's word for it, as this is not an implausible claim. In contrast, if someone else claimed that an elephant was in the backyard, the BoP would be on that claim, as I presume that elephants don't frequent my backyard―and so far this presumption has proven true. However, if the claim was that there was a unicorn in my backyard, the burden would be heavier, that is, it would take weightier evidence to convince me that a unicorn was in my backyard than that an elephant was there, because elephants exist but there's no such thing as a unicorn. So, some BoPs are heavier than others.
Turning now to the relation between the BoP and logical fallacies, Pigliucci is right about the fallacy of ad ignorantiam, as well as the fact that it's not always a fallacy to appeal to ignorance―a point that I emphasize in the entry for that fallacy. For instance, if someone claimed that there was an elephant in my backyard but offered no evidence, I would not commit a fallacy of appeal to ignorance by rejecting the claim for lack of evidence.
I suppose that circularity may be thought to fail to shift the BoP because the premisses are as implausible, or even more implausible, than the conclusion. However, explaining what's wrong with begging the question in terms of the BoP seems to miss what's distinctive about circular reasoning, namely, its circularity.
I wish that Pigliucci had chosen to explain the relationship between the BoP and the ad hominem fallacy, rather than leaving it as an exercise for the reader. I suppose that an ad hominem fails to shift the BoP, but so would any fallacious argument. Other than that, I'm stumped.
Sources:
Fallacies:
Via: Mark David Barnhill, "New and Noteworthy: Continuity Problem Edition", To Believe or Do, 5/1/2013
Correction (9/25/2019): I, rather than Pigliucci, was mistaken in the above highlighted text. He was right that giving a hypothesis a prior probability of 1 will, indeed, lead to its posterior probability on any evidence being 1, as well. So, it's perfectly reasonable to call such a prior probability "faith" in the hypothesis. This fact is a corollary of the fact, which I accepted above, that the posterior probability of a hypothesis will be zero if its prior probability is zero, which is an almost immediate consequence of Bayes' Theorem. The supposed counter-example that I gave is also incorrect, because if its hypothesis were true then using Bayes' theorem, as I tried to do, would involve dividing by zero. If you want to see proofs that the corollary is true and the counter-example is incorrect, see the Technical Appendix, below.
I haven't read all of Charles Wheelan's new book Naked Statistics yet, so I can't give a full review of it or an unqualified recommendation. However, from what I have read, it's very clearly written and the explanations are easy to understand. Wheelan is also the author of a previous book called Naked Economics, which I also haven't read, but I suppose that explains the odd title.
In the "Acknowledgments" (p.xvii), Wheelan writes that he was inspired by How to Lie with Statistics, but Naked Statistics is a much longer and apparently much more thorough discussion of the basics of statistics than Huff's skinny book. Wheelan concentrates on explaining the "whys" of statistics, exiling the math to appendices at the ends of chapters. However, I would recommend not skipping the mathematical appendices, even if you think you're bad at math. The math isn't especially hard and, in the appendices that I've read, Wheelan does an excellent job of explaining it.
The book discusses a number of familiar topics from these pages: "Assuming events are independent when they are not" (pp. 100-101), the gambler's fallacy (pp. 102-103), the prosecutor's fallacy (pp. 104-105), regression to the mean (pp. 105-107); correlation ≠ causation (pp. 215-216); there are explanations of several important biases, including publication bias (pp. 120-122); and there's an entire chapter on polls (ch. 10).
Source: Charles Wheelan, Naked Statistics: Stripping the Dread from the Data (2013)
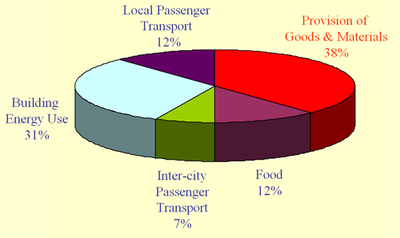
Pie charts are one of the most common and useful types of statistical graph. Often, the "pie" is simply a circle that has been divided into slice-shaped wedges, but sometimes a third dimension is introduced by slanting the pie away from the viewer, so that its edge can be seen.
Why add a third dimension to usually two-dimensional graphs? Typically, the added dimension adds no additional information, rather it seems to be done simply to make a prettier picture. Of course, there's nothing wrong with making a chart look better, but such changes should not distort the information contained in it.
For an example, take a look at the pie chart above and to the right, which is angled as if it were sitting on a table in front of you. From the thickness of its edge, it's obviously a deep-dish pie. Its slices represent the percentages of total greenhouse gas emissions from different types of activity. Notice, however, that the "Food" and "Local Passenger Transport" slices of the pie are an identical 12% of the whole, but the "Food" slice looks bigger because perspective puts it closer to you and you can see its edge, which adds area. Similarly, the smallest slice, "Inter-city Passenger Transport", looks larger than it should for the same reasons as the "Food" slice next to it―just imagine how much less noticeable it would be to the rear of the pie where you couldn't see its edge. Finally, the "Building Energy Use" slice is almost a third of the pie, but the angle at which it is shown makes it look like no more than a quarter.
Now, you might defend this chart on the grounds that the percentages represented by each slice are printed right by them, so how misleading can it be? However, the whole point of such a chart is to make it possible for the viewer to visually compare the sizes of the different slices of the pie, so it shouldn't be necessary to read the percentages so as not to be fooled. If you have to provide the numbers to avoid misleading the viewer, then it would be better to just give the numbers and leave out the chart.
The example chart may not have been intended to be misleading, but may have resulted from a graphics program that makes it easy to construct a chart in three dimensions. So, if you're a pie maker, and can't resist adding a third dimension to it, try to keep the angle of the pie away from the viewer as shallow as possible. We should be looking almost directly down at the pie, which should appear to be close to a circle. Also, the edge of the pie should not be too thick, as the thicker the edge the larger the pieces at the front of the pie will appear to be.
If you're a consumer of pie, be on the lookout for the three-dimensional kind. Keep in mind the visual distortions that may result from looking at the pie from a shallow angle, and pay close attention to the actual percentages if they are provided.
Sources:
Previous Entries in this Series:
Solution to the Puzzle of the Library Books: Cathy.
Since either Adam or Beth checks out a mystery novel, there are two possibilities. Let's suppose that Adam checks out a mystery. So, Cathy will check out a puzzle book, and then Beth will also select a mystery. However, we're given that Adam and Beth won't choose the same type of book, therefore our assumption is wrong: Adam does not select a mystery.
Thus, Beth always checks out a mystery. Since Adam and Beth don't choose the same kind of book, Adam always selects a puzzle book. Therefore, Cathy is the only one of the three who could have checked out different types of book on different trips to the library.
Technical Appendix: For those who know propositional logic, let's formalize the premisses that we're given:
Here's a truth-table showing that the only time all four premisses are true, rows five and six, A is false, B is true, and C is the only simple proposition that can take on both values. Thus, it is only Cathy who can check out a puzzle book one time and not at another time―meaning that she selects a mystery book, instead, since those are the only two choices possible.
Source: Paul Sloane, Des MacHale & Michael A. DiSpezio, The Ultimate Lateral & Critical Thinking Puzzle Book (2002). The puzzle was adapted from one on page 196.
Update (5/22/2013): Reader Sean Leather writes:
This ambiguity was not intentional but it doesn't affect the solution, as you point out, though it may make it a little harder. An explanation of the solution allowing for the possibility that a family member may not check out a book will be the same through the first paragraph above. Here's a revised second paragraph:
Thus, Beth always checks out a mystery. Since Adam and Beth don't choose the same kind of book, either Adam always selects a puzzle book or he checks out no book at all. Therefore, Cathy is the only one of the three who could have checked out different types of book on different trips to the library.
Technical Appendix for the Correction: For those interested in the details, here's a proof of the claim that a prior probability of 1 leads to a posterior probability of 1 on any evidence, and that the counter-example fails. I use the axiom system outlined in the entry on Probabilistic Fallacy: see the fallacy menu to the left.
Lemma: P(h | e) + P(~h | e) = 1, if P(e) ≠ 0.
Proof:
P(h | e) + P(~h | e) = P(h & e)/P(e) + P(~h & e)/P(e), by Axiom 4 and the hypothesis that P(e) ≠ 0.
P(h & e)/P(e) + P(~h & e)/P(e) = [P(h & e) + P(~h & e)]/P(e), since the addends share a denominator.
[P(h & e) + P(~h & e)]/P(e) = P[(h & e) v (~h & e)]/P(e), by Axiom 3 and the fact that (h & e) and (~h & e) are contraries.
P[(h & e) v (~h & e)]/P(e) = P[e & (h v ~h)]/P(e), by logical distribution.
P[e & (h v ~h)]/P(e) = P(e)/P(e), since [e & (h v ~h)] is logically equivalent to e.
P(e)/P(e) = 1, which completes the proof.
An immediate corollary of the lemma is:
Corollary: P(~h | e) = 1 - P(h | e), if P(e) ≠ 0.
Now, we have what we need to prove the theorem:
Theorem: If P(h) = 1 and P(e) ≠ 0, then P(h | e) = 1.
Proof:
Theorem: If P(h) = 1 and P(e | h) = 0, then P(e) = 0.
Proof: Suppose that P(h) = 1 and P(e | h) = 0.
If P(e) = 0 then Bayes' theorem cannot be used as I tried to do in the counter-example, since division by zero is undefined.
May 11th, 2013 (Permalink)
New Book: Naked Statistics
May 5th, 2013 (Permalink)
Charts & Graphs: Three-Dimensional Pie
A B C A v B A → C C → B ∼ (A & B) T T T T T T F T T F T F T F T F T T T F T T F F T F T T F T T T T T T F T F T T T T F F T F T F T F F F F T T T The puzzle in the subject is a bit vague in one regard. You say: "They always check out either mysteries or puzzle books, but never more than one book apiece." Here, "they always check out [...] books" can mean that the family, as a whole, checks out N books, where N > 0. The second clause says that each member checks out at most 1 book. This can lead to the conclusion that each family member has 3 states (mystery, puzzle, none) instead of the 2 given in the solution. As far as I can tell, no other statement in the puzzle removes this ambiguity. This is a typical ambiguity with using "they" in English. A less ambiguous phrasing for the sentence above might be: "Each person always checks out one book which is either a mystery or a puzzle book." In the case of 3 states, the answer to the question: "Who checked out a mystery on one trip to the library but a puzzle book a different time?" is the same as the given solution, though the logic is a bit more complex. Consequently, it would still be nice to have a less ambiguous problem description.