WEBLOG

Previous Month | RSS/XML | Current | Next Month

November 28th, 2013 (Permalink)

Thanks!

On this day of thanks, I am thankful for all of you who have supported this website over the last year, whether by visiting the site's advertisers, buying something through the links to Amazon, or donating directly via PayPal. Thank you!

Update (2/16/2021): The Fallacy Files is no longer an Amazon associate, so please do not try to support the site by purchasing through any remaining Amazon ads.

November 21st, 2013 (Permalink)

Check it Out

I have a couple of comments about William Saletan's interesting article in Slate on psychological research into conspiracy theorizing:

I find it plausible that people who believe one conspiracy theory are more likely to believe another one, even if it's completely unrelated. After all, one problem with conspiracy theorizing is the lowering of evidential standards, and if you lower your standards enough to let in one conspiracy theory, you're bound to let in others. However, I would not have thought that belief in one conspiracy theory would make you more likely to believe another, contrary theory. Perhaps conspiracy theorists have so compartmentalized their beliefs that they can hold two contrary beliefs at the same time.
At the end of the article, Saletan writes:
Psychologists and political scientists have repeatedly demonstrated that “when processing pro and con information on an issue, people actively denigrate the information with which they disagree while accepting compatible information almost at face value.” Scholars call this pervasive tendency “motivated skepticism.” Conspiracy believers are the ultimate motivated skeptics.

From Saletan's brief description, motivated skepticism sounds like a type of confirmation bias. Some psychologists use the phrase "motivated reasoning" for what appears to be a combination of wishful thinking―that's the "motivation" part―and confirmation bias. So, I suppose that motivated skepticism is motivated reasoning when it takes the form of doubt about something.
If that's the case, then the motivation part is missing from Saletan's description, that is, a motivated skeptic is skeptical only about things the "skeptic" doesn't want to believe. Whereas, if anything, we should all be more skeptical of those things we want to believe. However, this doesn't explain why conspiracy theorists would be motivated to believe their theories, since this leads them to some strange beliefs. Why anyone would want to believe most conspiracy theories is still a mystery.
The process that Saletan describes is not completely unreasonable. We all know many things, and so many candidate beliefs are vying for our attention that we don't have the time or energy to subject them all to careful scrutiny. As a result, it makes sense to pass them first through a filter that screens out things that we already know are false.
Of course, the danger is that this filter should become a barrier to any new information that challenges our existing beliefs. Among our many beliefs are bound to be some false ones, but if we screen out all candidate beliefs that conflict with any of our existing beliefs, we'll never be able to correct our mistakes. So, the filter needs to be porous enough to allow us to change our minds when sufficient evidence has accumulated.
The problem with conspiracy theorists would seem to be that their filters have become so impervious to contrary information that they're never able to correct their false beliefs. Meanwhile, the same filters are so porous to information that is consistent with their existing false beliefs that those beliefs may act as magnets to attract new false beliefs. This is probably why arguing with them often seems to be a futile endeavor!

Source: William Saletan, "Conspiracy Theorists Aren’t Really Skeptics", Slate, 11/19/2013

Reader Response (12/6/2013): A reader who would rather remain nameless writes:

There is a confirmation bias on the part of all parties. Usually this is put in terms of conspiracy theorist or not conspiracy theorist. This type of either/or reasoning is fallacious. Does this definition suit you? Conspiracy: two or more parties coming together to the detriment of a third party. Conspiracies happen quite often. The term conspiracy theorist has become a sort of ad hominem that allows people to ignore certain lines of logic. (Guilt by association?)

I have a few points to make in response. First off, a couple of minor ones:

Yes, confirmation bias is a general human problem, and I hope that you didn't get the impression that I was claiming otherwise in what I wrote above. I think that if you reread it carefully, you'll see that I never suggested that conspiracy believers were worse than anyone else in that regard. It wouldn't surprise me if they were, but I don't have any evidence to that effect. Moreover, in the last three paragraphs above, I tried to explain that the process that some psychologists call "confirmation bias" is a rational one if not taken to an extreme. I do think that conspiracy theorists and other pseudoscientists take it to an extreme, but they're certainly not alone in that.
"Either/or reasoning" is only fallacious when there is some third possibility left out, but it would seem that you're either a conspiracy theorist or you're not. Of course, there may be the third possibility that you're a borderline case, since "conspiracy theorist" is a vague concept. That said, I don't see how this is relevant to what I wrote.
The main point that I want to address is the definition of "conspiracy theory": you seem to be suggesting a point that I've heard previously by conspiracy believers, namely, that a conspiracy theory is just a theory about a conspiracy. That, of course, is what the phrase "conspiracy theory" might lead you to believe, but that is not what it has come to mean. Rather, "conspiracy theory" is an idiom, so that you can't figure out the meaning of the phrase simply from its component words. Of course, part of the meaning of "conspiracy theory" is a theory involving a conspiracy, but that's not the important part.
Conspiracy theories are not real theories at all, but pseudotheories that involve conspiracies. Here I use the term "pseudotheory" in somewhat the same way that "pseudoscience" is used, and this is appropriate because pseudotheories and pseudoscience are closely related. Just as a pseudoscience is a non-science that pretends to be scientific, so a pseudotheory is a non-theory that imitates a true theory.
In what way do conspiracy theories fail to be genuine theories? They fail the test of falsifiability that the philosopher Karl Popper pointed to as an important characteristic of scientific theories, that is, they fail to make predictions that can be shown false. In this way, pseudotheories are connected to pseudoscience, since it is falsifiability that marks the difference between science and nonscience, according to Popper. This isn't to endorse Popper's views in their entirety, by the way, but he was correct that falsifiability is an important characteristic of a theory, because an unfalsifiable theory lacks empirical content.
Of course, a theory about a conspiracy isn't inherently unfalsifiable; rather, it's the way that a conspiracy theory is held that turns it into a pseudotheory. Conspiracy theorists, like pseudoscientists, protect their theories from refutation by various ad hoc ploys that have the cumulative effect of emptying them of content.
Theories about conspiracies are always in particular danger―more so than other types of theory―of turning into unfalsifiable pseudotheories. This is because the conspiracies metastasize and counterevidence is attributed to the conspiracy, or to a secondary conspiracy designed to cover-up the original conspiracy.
I came across a perfect example of this process at work while researching the Jamie McIntyre contextomy (see the Resource, below): As noted in the entry on that quote, in a later interview McIntyre stated that he had been quoted out of context. However, instead of admitting that in this case McIntyre had been quoted in a misleading way, some conspiracy theorists claim that someone had "got to" him and forced him to lie about what he had earlier said. This, despite the fact that the original video shows what he later said to be correct.
This also explains why arguing with conspiracy theorists can be as headache-inducing as running headfirst into a brick wall. Evidence that shows the theory to be incorrect is simply dismissed as itself part of a larger conspiracy to cover-up the original conspiracy. If you can escape from such an argument without being accused of being part of the conspiracy yourself, you're lucky!

In conclusion, I'm reminded of the following passage from Plato's Republic:

…[Y]oungsters, as you may have observed, when they first get the taste in their mouths, argue for amusement, and are always contradicting and refuting others in imitation of those who refute them; like puppy-dogs, they rejoice in pulling and tearing at all who come near them. … And when they have made many conquests and received defeats at the hands of many, they violently and speedily get into a way of not believing anything which they believed before, and hence, not only they, but philosophy and all that relates to it is apt to have a bad name with the rest of the world.

Source: Plato, The Republic, Book VII, 539b-c

Resource: Familiar Contextomies: Jamie McIntyre

Fallacies:

November 19th, 2013 (Permalink)

Charts & Graphs: The YY Graph

The sin of a "double Y-axis graph" is mortal. If there is a just God, I am sure that there is a special place in the inferno reserved for its perpetrators.―Howard Wainer (P. 91)

A double-Y―or dual-Y―axis graph is a Cartesian graph, that is, a graph with X and Y axes. Typically, such graphs are rectangular with the bottom of the graph representing the X-axis―or abscissa―and the left-hand side representing the Y-axis―or ordinate. A double-Y axis is, of course, such a graph with two Y-axes, where the second Y-axis is represented by the right side of the rectangle.

If you think about it for a moment, a Cartesian graph with two Y-axes is impossible! However, a double-Y axis graph is, in effect, two Cartesian graphs with a common X-axis laid one on top of the other. Despite what Wainer, author of Visual Revelations, says in the quote above―I just thought it was funny―there isn't anything necessarily wrong with YY graphs. Even Wainer goes on, at the end of the chapter where he discusses them to write:

Is there any use of the double Y-axis format that is reasonable? A very restricted "yes." (P. 94)

Anytime you want to compare two Cartesian graphs that share an X-axis, it might make sense to combine them into a single YY graph. However, the danger of such graphs is that it's very easy to manipulate the two Y-axis scales to create a misleading impression.

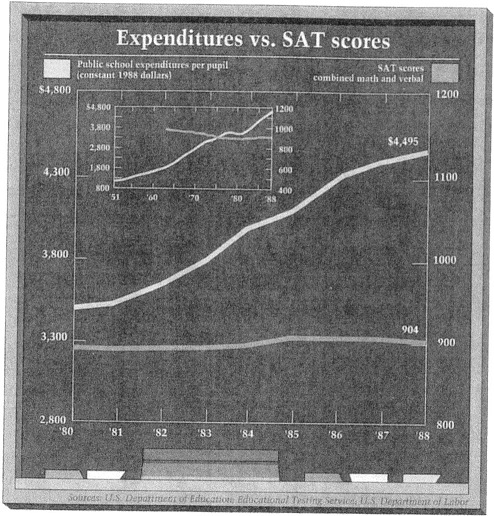
Consider the example above, which comes from Wainer's book (p. 93), though it originally appeared in Forbes magazine on May 14th, 1990. Ignoring the small inset graph, the main graph compares school spending with Scholastic Aptitude Test (SAT) scores over the course of the nine years from 1980 to 1988. Just glancing at it, you'd get the impression that spending went up but SAT scores remained relatively flat, which may be just the impression that the chart-maker intended. The left-hand Y-axis representing per pupil spending starts at $2,800 and goes to $4,800; whereas the right-hand Y-axis for combined math and verbal scores on the SAT starts at 800 and extends to 1200, though a low of 400 and a high of 1600 total points are possible.

So, this chart is two gee-whiz line graphs in one! (See the first entry in the series, below, if you don't know what I'm talking about.) The left-hand scale seems to have been chosen to exaggerate the degree to which spending has risen, so that the rise takes up about half of the vertical space of the graph. In contrast, the right-hand scale flattens out the rise in SAT scores by including a larger part of the scale. The increase in spending over nine years is about $1,000 per pupil, while the scores increased around fourteen points, though it's hard to tell exactly. Depending on how much each scale is squeezed or stretched, it would be possible to make both lines almost parallel, or even to switch their positions, so that it would appear that spending barely increased while the scores soared.

This is one problem with YY graphs: the impression that they create is easily manipulated by placing a finger on the scales. So, when confronted with a graph with two Y-axes, carefully examine each scale: has one been stretched in order to create a "gee-whiz" reaction, or squeezed to play down a change?

Another problem is that simply graphing two variables on the same graph may create the impression of a causal relationship, especially if the Y-axes have been carefully tweaked to make the lines parallel. So, always ask yourself whether such a causal relationship is plausible and, if so, which direction does it go? Is it possible that both variables are affected by a third one that isn't graphed?

If you ask and can answer these questions, you should avoid being deceived by a YY-graph.

Source: Howard Wainer, Visual Revelations: Graphical Tales of Fate and Deception from Napoleon Bonaparte to Ross Perot (1997), Chapter 9: "Double Y-Axis Graphs"

Previous entries in this series:

The Gee-Whiz Line Graph, 3/21/2013
The Gee-Whiz Bar Graph, 4/4/2013
Three-Dimensional Pie, 5/5/2013
The 3D Bar Chart, Part 1, 6/3/2013
The 3D Bar Chart, Part 2, 7/11/2013
The One-Dimensional Pictograph, 8/1/2013
A Charts & Graphs Pop Quiz, 9/15/2013
"I see a little silhouette-o of a man", 10/19/2013

November 17th, 2013 (Permalink)

Quote…

While we have seen the apparent death of Communism, ways of thinking that were either born under Communism or strengthened by Communism still govern our lives. Not all of them are as immediately evident as a legacy of Communism as political correctness. The first point: language. It is not a new thought that Communism debased language and, with language, thought. There is a Communist jargon recognizable after a single sentence. Few people in Europe have not joked in their time about “concrete steps,” “contradictions,” “the interpenetration of opposites,” and the rest. … Even five, six years ago, Izvestia, Pravda and a thousand other Communist papers were written in a language that seemed designed to fill up as much space as possible without actually saying anything. Because, of course, it was dangerous to take up positions that might have to be defended. Now all these newspapers have rediscovered the use of language. But the heritage of dead and empty language these days is to be found in academia…. Yes, I know the obfuscations of academia did not begin with Communism―as Swift, for one, tells us―but the pedantries and verbosity of Communism had their roots in German academia. And now that has become a kind of mildew blighting the whole world. … The phrase “political correctness” was born as Communism was collapsing. I do not think this was chance. I am not suggesting that the torch of Communism has been handed on to the political correctors. I am suggesting that habits of mind have been absorbed, often without knowing it. … I am sure that millions of people, the rug of Communism pulled out from under them, are searching frantically, and perhaps not even knowing it, for another dogma.―Doris Lessing (6/26/1992)

…Unquote

Source: Doris Lessing, "Questions You Should Never Ask a Writer", The New York Times, 10/13/2007

GOD DOES NOT BELIEVE IN ATHEISTS THEREFORE ATHEISTS DO NOT EXIST

November 15th, 2013 (Permalink)

Gödel's God

Here are some headlines from the end of last month:

Scientists Prove God Exists

Scientists Prove God Exists and Here's the Proof

How Modal Logic Proved Gödel was Right, and God Exists

Why didn't this story get more attention? If true, isn't this the biggest news in human history, or at least the last month? Some other headlines for the same story put the word "prove" in quotation marks, or otherwise suggest some doubt about it, but I purposely chose those that present it as an established fact.

Kurt Gödel was a famous 20th-century logician, and the proof in question comes from his unpublished notebooks. Gödel died in 1978, but the proof became public in 1970 through another famous logician, Dana Scott, who knew Gödel. The argument is one of a class of similar ones called "ontological" by philosophers, and in my experience they are more confusing than convincing. An ontological argument for the existence of God is rather like a magician pulling a rabbit out of a hat: it's surprising that a rabbit comes out of the hat, and you may not know exactly how the rabbit got in there, but you don't really believe that it just appeared out of thin air. Similarly, it's surprising when at the end of an ontological argument God pops out, but you don't really believe it. Somehow, just as the magician manages to slip a rabbit into the hat when you're not looking, the philosopher is able to slip the existence of God into the premisses.

The third headline above, as well as other articles, mentions that the proof uses modal logic, but this doesn't mean that the existence of a god is a theorem of modal logic. It's not. Modal logic, in this case, refers to the logic of the related notions of necessity and possibility―there are other modalities, see the entry for "Modal Fallacy" in the drop-down menu to your left for more on modalities and their logic. The conclusion of Gödel's proof is that a god necessarily exists―which, of course, entails that a god exists―and it's this use of the notion of necessity that requires modal logic. Rather than being a theorem in some system of modal logic, the conclusion is a theorem in an axiom system created by Gödel, but really it's just an argument with eight premisses.

Some of the news articles and their headlines seem to suggest that it's been proven for the first time, but I don't think that there's ever been much doubt that the proof is correct. It's challenging, but not so hard that it requires a computer to do. Gödel's much more famous and important incompleteness theorem is far more difficult!

Instead, the authors of the two-page article upon which all of the news stories are based (see Source 1, below) were reporting an achievement in automated theorem proving, not the first proof of the existence of a god. Apparently, proof of the argument was a difficult challenge for such programs, presumably because of the use of modalities but perhaps also second-order quantifiers―that is, quantifiers that range over properties instead of individuals―which also play a role in the proof.

So, what exactly did Gödel prove? The proposition in question really was proven, so the headlines are right to say so. However, it was proven from the premisses given by Gödel, and it's in the interpretation of those premisses that the problem of what to make of it all lies. In fact, since all five of the "axioms" make use of an undefined predicate, it's not even clear what they mean. Calling it a proof of the existence of God is one interpretation, and it was presumably Gödel's interpretation, but it's not the only possible interpretation, nor is it forced on the skeptic. The premisses are not at all like the axioms of logic or mathematics, that is, they're not self-evidently true nor does denying one lead to self-contradiction. All that anyone who doubts the existence of a god needs to do is reject one or more of the axioms.

Sources:

Christoph Benzmüller & Bruno Woltzenlogel Paleo, "Formalization, Mechanization and Automation of Gödel’s Proof of God’s Existence", Arxiv, 9/10/2013 (PDF)
Roxanne "Butter" Bracco, "Scientists Prove God Exists: An Austrian Math Model, a Macbook and Now Artificial Intelligence", The Global Dispatch, 10/31/2013
Elke Brendel, "Gödel's Ontological Proof of the Existence of God"
Mike DeHaan, "How Modal Logic Proved Gödel was Right, and God Exists", Decoded Science, 10/31/2013
Staff Reporter, "Scientists Prove God Exists and Here's the Proof", Parent Herald, 10/31/2013

Resource: There ain't no such thing as a free lunch in logic!, 4/26/2013

November 10th, 2013 (Permalink)

New Book Reviews

(11/13/2013) Another new book that I pointed out earlier this year (see the Resource, below)―pediatrician Paul Offit's Do You Believe in Magic?―has been given a rave by Harriet Hall, a retired physician who writes on medical matters for Skeptical Inquirer (see the Source, below). According to Hall, there's some unsurprising fallacy overlap with Science Left Behind:
[Offit] explains why alternative therapies are popular: mainstream doctors are perceived as uncaring and dictatorial, offering unnatural remedies with intolerable side effects, while alternative healers provide natural remedies, comfort, and individual attention. But he warns that “natural” remedies mustn’t be given a free pass. Unless we hold all therapies to the same high standard of scientific proof, we risk being hoodwinked by healers who believe in magic.

Another familiar fallacy puts in an appearance:
[Offit] eviscerates Suzanne Somers for her anti-aging regimen and Jenny McCarthy for her crusade against vaccines. … He builds on Steve Jobs’s flirtation with alternative treatments for his pancreatic cancer to cover the larger story of bogus cancer cures, from shark cartilage to Krebiozen to Gerson therapy.

Source: Harriet Hall, "Do You Believe in Magic? Book Review", Skeptical Inquirer, July/August 2013
Resource: New Book: Do You Believe in Magic?, 7/10/2013
I mentioned the newish book―it turns out that it was published last year―Science Left Behind earlier this year (see the Resource below). Eskeptic has a favorable review by Kenneth Krause, an editor and columnist for both The Humanist and Skeptical Inquirer magazines. Here's what Krause has to say about the book's discussion of a familiar fallacy:
[The authors] accuse progressives of propagating a number of socially destructive myths, among them the assumptions that everything “natural” is good and everything “unnatural” is bad. Accordingly, homeopathy is just as good as or better than traditional medicine, vaccines actually harm children, and nuclear energy promises unprecedented sickness and loss of life. And despite studies showing conventional crops to be equally nutritional and both personally and environmentally safe (never mind vastly less expensive), “organic” foods…are somehow superior products. Ditto for raw, unpasteurized dairy products and juices left untreated for foodborne illnesses. Meanwhile, genetically modified foods are decried as both personal and environmental menaces. Never mind that years of testing has yielded no evidence of risk.

Check it out.
Source: Kenneth W. Krause, "The Progressive War on Science", Eskeptic, 3/13/2013
Resource: Check it Out, 2/18/2013
Update (11/14/2013): There's more on the Left's "war" against science from Mischa Fisher in The Atlantic of all places.
Source: Mischa Fisher, "The Republican Party Isn't Really the Anti-Science Party", The Atlantic, 11/11/2013

Fallacies:

November 5th, 2013 (Permalink)

Headline

Far-Off Planets Like the Earth Dot the Galaxy

Via: Glenn Reynolds, "But wait, the Earth's not far off. It's right here!", Instapundit, 10/5/2013